There's no Archery without Aim!
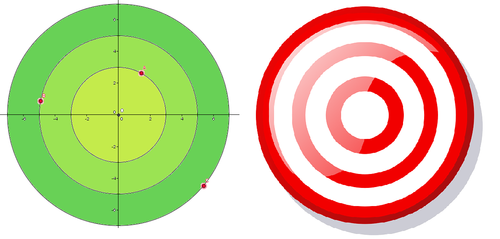There are 3 concentric circles with center
O
and radii
3
,
5
,
7
units.
Points A , B , C are on these circles, one on each circle.
Find the minimum value of A B 2 + B C 2 + C A 2 in sq. units.
Also see
The answer is 24.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Note that in general, it is not necessarily true that "(minimum will occur) when (AB is minimum and BC is minimum and CA is minimum)"
Instead, what you should say is that A B ≥ 2 , B C ≥ 2 , C A ≥ 4 and thus A B 2 + B C 2 + C A 2 ≥ 4 + 4 + 1 6 = 2 4 . We can verify that this is achieved at A ( 3 , 0 ) , B ( 5 , 0 ) , C ( 7 , 0 ) .
Log in to reply
What is the maximum then?
Log in to reply
What do you think the answer is? How would you approach that problem?
You can solve the problem here .
What is the maximum then?
We can easily see that the shortest distance between to points on the circumference of two concentric circles is when they are on the same radial line on the same side of the center, and their distance is the difference beteen the two radii..
So if A is on circle with radius 3. B with 5, C with 7, we have:-
On any radial line on the same side of the center, AB=5-3=2,~~~BC=7-5=2~~~AC=7-3=4.
∴
A
B
2
+
B
C
2
+
A
C
2
=
4
+
4
+
1
6
=
2
4
.
For maximum distance as above between to points would be on same diameter but on opposite side of the center with distance = sum of their radii.. If there is a third point, we have two options. Two points on the circles with bigger radii, should be on the opposite sides of the center. The one on the smallest circle has two positions on the same diameter. Both have to be checked to see which gives maximum. Depends on the relative radial distances.
Minimum Will Occure when AB is minimum and BC is minimum and also CA is minumum. So Clearly It is Possible only when A,B,C are collinear. Hence Take A ( 3 , 0 ) B ( 5 , 0 ) C ( 7 , 0 )