There's No "Squared" Here
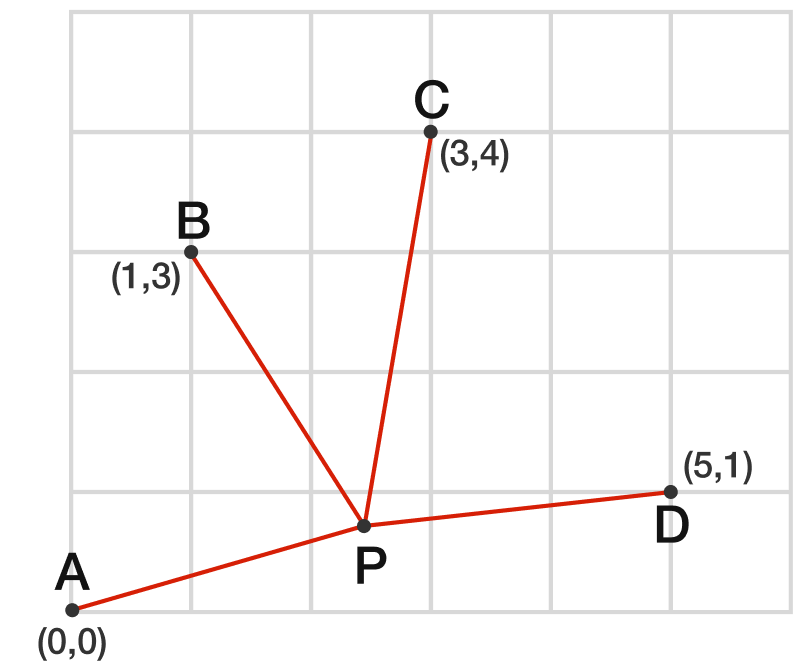
A = ( 0 , 0 ) , B = ( 1 , 3 ) , C = ( 3 , 4 ) , D = ( 5 , 1 )
Minimize the sum of the lengths of P A + P B + P C + P D .
This value can be written as X + Y , where X and Y are positive integers; submit your answer as X + Y .
The answer is 25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
In a convex quadrilateral the shortest path that connects all vertexes is the sum of the two diagonals.
These are AC and BD.
A
C
=
3
2
+
4
2
=
5
,
a
n
d
B
D
=
(
3
−
1
)
2
+
(
1
−
5
)
2
=
2
0
.
S
o
f
o
r
m
i
n
i
m
u
m
(
P
A
+
P
C
)
+
(
P
B
+
P
D
)
=
A
C
+
B
D
=
5
+
2
0
=
X
+
Y
.
S
o
X
+
Y
=
5
+
2
0
=
2
5
.
N
o
n
e
e
d
t
o
l
o
c
a
t
e
P
.
The first line is true for a convex quadrilateral. For a concave quadrilateral, the answer is quite different.
Log in to reply
Thanks. I have corrected.
What would be the minimum for a concave quadrilateral?
If the four points A , B , C , D form a convex quadrilateral, we see that, for any point P A P + P C ≥ A C B P + P D ≥ B D with equality when A , P , C and B , P , D are collinear. Thus we deduce that A P + B P + C P + D P ≥ A C + B D with equality when P is the point of intersection of A C and B D .
In this case, the point of intersection is ( 1 1 2 1 , 1 1 2 8 ) , and the shortest sum of distances is 5 + 2 0 , making the answer 5 + 2 0 = 2 5 .