Thermodynamic cycle
An ideal gas goes through a thermodynamic cycle with the following steps
- Isobaric compression from an initial volume of to at a pressure of .
- Isochoric pressure increase.
- Isothermal expansion back to the initial state.
What is the amount of total work that the gas does in one cycle?
Specify the result in units of joules and round to the nearest integer.
The picture below shows a possible implementation of this cycle in a kind of Stirling engine. The gas is in a tube that is heated at the top and cooled at the bottom. A displacement piston pumps the gas back and forth between the two heat baths, without doing any work. Only in isobaric compression and isothermal expansion the volume changes and work is done.
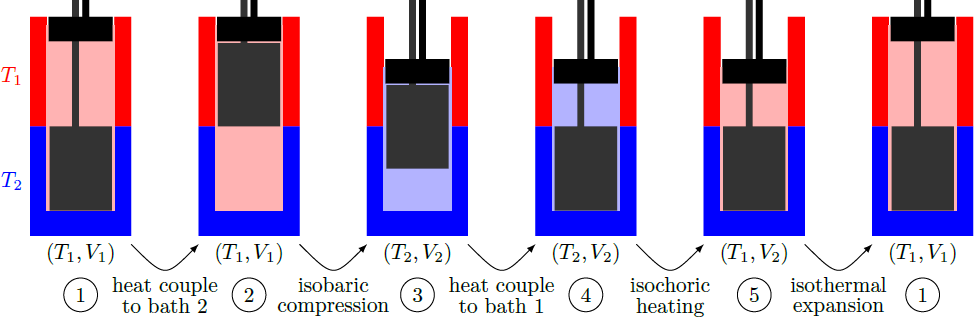
The answer is 309.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The thermodynamic cycle can be represented in the pressure-volume diagram by the following curve: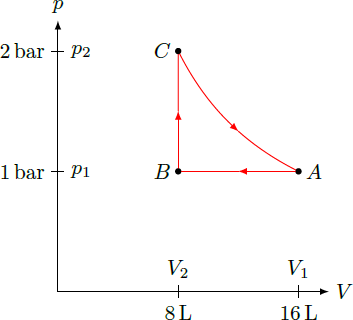 The points
A
=
(
V
1
,
p
1
)
and
B
=
(
V
2
,
p
1
)
have been given directly. The pressure at the point
C
=
(
V
2
,
p
2
)
results from the fact that we reach the initial state
A
in the last step by isothermal expansion. Thus
p
2
V
2
=
p
1
V
1
and hence
p
2
=
V
2
V
1
p
1
=
2
bar
.
The points
A
=
(
V
1
,
p
1
)
and
B
=
(
V
2
,
p
1
)
have been given directly. The pressure at the point
C
=
(
V
2
,
p
2
)
results from the fact that we reach the initial state
A
in the last step by isothermal expansion. Thus
p
2
V
2
=
p
1
V
1
and hence
p
2
=
V
2
V
1
p
1
=
2
bar
.
The mechanical work of the gas corresponds to the area enclosed by the curve in the pressure-volume diagram and is calculated by the integral W = ∮ p d V = ∫ A → B p d V + ∫ B → C p d V + ∫ C → A p d V = p 1 ( V 2 − V 1 ) + 0 + ∫ V 2 V 1 V p 1 V 1 d V = − 2 1 p 1 V 1 + p 1 V 1 lo g V 2 V 1 = p 1 V 1 ( lo g ( 2 ) − 2 1 ) = 1 bar ⋅ 1 6 L ⋅ ( lo g ( 2 ) − 2 1 ) = 1 0 5 Pa ⋅ 0 . 0 1 6 m 3 ⋅ ( lo g ( 2 ) − 2 1 ) ≈ 3 0 9 J