Thermodynamics 14-10-2020

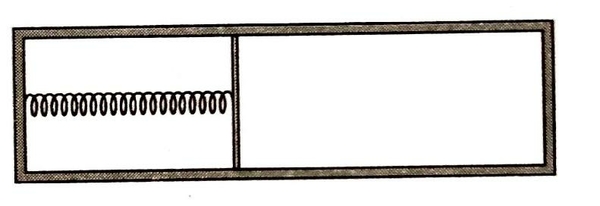
Classical Mechanics Level pending

A heat-conducting piston connected with the help of a spring to one end of a horizontal closed insulated cylinder divides the cylinder into two parts. Each part of the cylinder contains equal number of moles of amono-atomic ideal gas. The length of the cylinder is 2 l 2l and relaxed length of the spring is l 2 \frac{l}{2} .

Initially temperature of the gas in both the parts is T T extension in springs is x 0 x_{0} and the piston is in equilibrium. Now a hole is made in the piston. If heat capacities of the cylinder, the piston and the spring are negligible,

Find change in the temperature of the gas after establishment of new equilibrium state.
Answer comes in the form of α x 0 T β ( l − α x 0 ( l + α x 0 ) ( β l − α x 0 ) ) \frac{\alpha x_{0}T}{\beta}(\frac{l-\alpha x_{0}}{(l+\alpha x_{0}) (\beta l-\alpha x_{0})})
Type α + β = ? \alpha+\beta=?


The answer is 5.

Talulah Riley by Talulah Riley , 18, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Talulah Riley
Oct 14, 2020


Summary: Initially the spring force was balanced by the unbalanced forces of the pressures of the gases on both sides of the piston. This fact provides information about the force constant of the spring and energy stored in the spring.
Since the system consisting both the parts is a closed system of constant volume, during the process taking place after the hole is made, the total energy stored in the spring is utilized in increasing the internal energy of the gas.

Feel free to ask me anything regarding the solution.

1 Helpful 1 Interesting 1 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...