Thermodynamics
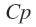
The constant-volume heat capacity of a gas can be measured by observing the decrease in temperature when it expands adiabatically and reversibly. If the decrease in pressure is also measured, we can use it to infer the value of γ = Cp /CV and hence, by combining the two values, deduce the constant-pressure heat capacity. A fluorocarbon gas was allowed to expand reversibly and adiabatically to twice its volume; as a result, the temperature fell from 298.15 K to 248.44 K and its pressure fell from 202.94 kPa to 81.840 kPa. Evaluate Cp.
Note: This question is from a well renowned book.
The answer is 41.4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
You can directly do it by using
P f P i = ( T f T i ) R C P
Why can't we use C p = C v + R ?
Log in to reply
The equation C p = C v + R is for a constant pressure process.
Cp=r(gamma)/(gamma-1) this makes the question very easy
Log in to reply
But the equation is for constant pressure. It is derived from C p = C v + R .
Where do you derive your very first equation from?
V T R C V = constant
Edit: Nevermind, found it. I somehow never saw this equation in relation to the adiabatic process. To everyone else look here for reference:
[1] Atkins; De Paula (2006). Physical Chemistry (8th ed.). Oxford university press. p. 48. ISBN 0-7167-8759-8.
Log in to reply
Note that the "Note" in the problem said that the problem was from a renowned book I managed to find the book online and check out the problem. The answer was given but not the solution. I got the equation from that book.
In adiabatic process,
for 1 mol ideal gas:
Cv dT= - Pext dV
simplify this, integrate to get
Cv ln(Tf/Ti) = - R ln(Vf/Vi)
Cv ln(Tf/Ti) = R ln(Vi/Vf)
ln(Tf/Ti) = (y-1) ln(Vi/Vf)
Tf/Ti = (Vi/Vf)^(y-1)
(Tf).(Vf)^(y-1) = (Ti).(Vi)^(y-1)
(T).(V)^[(Cp/Cv) - 1] = constant
(T).(V)^[(Cp - Cv)/Cv] = constant
(T).(V)^[R/Cv] = constant
Should have given unit to ans in
I Have A Question( A Few Actually)... Why Is Carbon A Good ingredient For Organic Matter? Why Does Salt Prevent The Growth Of Bacteria? Why Does K React More Vigorously In Water Than Na? Why Do We Salt Roads In The Winter? Why Doesn't Pure Water Conduct Electricity? Why is it important that scuba divers ascend to the surface slowly and gradually? ...... Detailed Answers Would Be Appreciated From Anyone Who Can Help. ☺
Log in to reply
Why don't you google to find out?
You are suggested to publish it in a note......go to publish and select note and type your note
Assuming that the fluorocarbon gas behaves as an ideal gas, then it follows:
{ V T R C V = constant p V γ = constant . . . ( 1 ) r e v ∘ . . . ( 2 ) r e v ∘
where R = 8 . 3 1 4 5 J mol − 1 K − 1 , the universal gas constant γ = C V C P C P = heat capacity at constant pressure C V = heat capacity at constant volume
( 1 ) : V i T i R C V T i R C V ⇒ C V ( 2 ) : p i V i γ p i ⇒ γ ⇒ C P = V f T f R C V = 2 T f R C V = lo g ( T f T i ) R lo g 2 = p f V f γ = 2 γ p f = lo g 2 lo g ( p f p i ) = lo g 2 lo g ( p f p i ) C V = lo g ( T f T i ) R lo g ( p f p i ) = lo g ( 2 4 8 . 4 4 2 9 8 . 1 5 ) 8 . 3 1 4 5 lo g ( 8 1 . 8 4 0 2 0 2 . 9 4 ) = 4 1 . 4 0 J mol − 1 K − 1