Just The Right Amount of Constraints
⎩ ⎨ ⎧ a + b + c = 5 0 3 a + b − c = 7 0
a , b and c are positive numbers satisfying the system of equations above.
If the range of 5 a + 4 b + 2 c is ( m , n ) , what is m + n ?
The answer is 400.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Good perfect solution..+1
Interpret the two given equations as planes in the 3D-Cartesian system. The allowed values would be a line segment (because the coordinates has to be positive). Call this line segment l . Solving the given equations along with:
(i) a = 0 gives a = 0 , b = 6 0 , c = − 1 0
(ii) b = 0 gives a = 3 0 , b = 0 , c = 2 0
(iii) c = 0 gives a = 1 0 , b = 4 0 , c = 0
Case (i) involves negative values, so it is rejected. Hence the endpoints of l are given by (ii) and (iii). 5 a + 4 b + 2 c = k is also describes a plane P for some constant k , that is always perpendicular to the vector ( 5 , 4 , 2 ) . Since all relationships are linear, the extreme values of k can be found relating it with the endpoints found before, i.e. (ii) 5 ∗ 3 0 + 4 ∗ 0 + 2 ∗ 2 0 = 1 9 0 and (iii) 5 ∗ 1 0 + 4 ∗ 4 0 + 2 ∗ 0 = 2 1 0 . (This can be interpreted as sliding a point along l at constant speed, and also sliding the plane p with the restriction that p has to contain the point, then k should vary linearly as the point slides from one endpoint of l to the other.) Hence the answer is 1 9 0 + 2 1 0 = 4 0 0 .

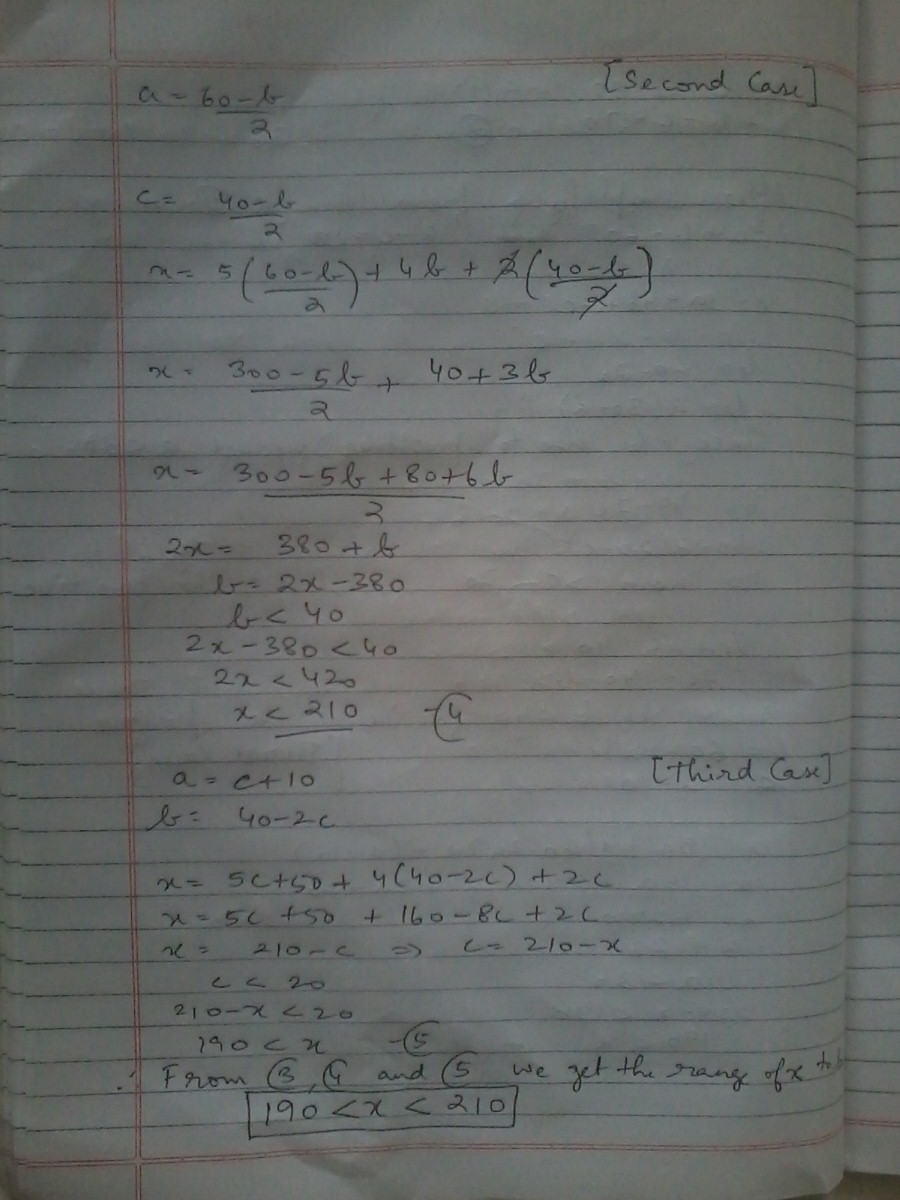
We first note that
(i) ( a + b + c ) + ( 3 a + b − c ) = 5 0 + 7 0 ⟹ 4 a + 2 b = 1 2 0 ⟹ 2 a + b = 6 0 ⟹ b = 6 0 − 2 a ,
(ii) ( 3 a + b − c ) − ( a + b + c ) = 7 0 − 5 0 ⟹ 2 a − 2 c = 2 0 ⟹ a − c = 1 0 ⟹ c = a − 1 0 .
Thus 5 a + 4 b + 2 c = 5 a + 4 ( 6 0 − 2 a ) + 2 ( a − 1 0 ) = − a + 2 2 0 .
Now as b > 0 we can infer from 2 a + b = 6 0 that a < 3 0 , and as c > 0 we can infer from a − c = 1 0 that a > 1 0 . So 1 0 < a < 3 0 ⟹ 1 9 0 < − a + 2 2 0 < 2 1 0 , and thus m + n = 1 9 0 + 2 1 0 = 4 0 0 .