These guys are increasingly same

Multiplying the given equation by "k" on both sides..... We get a quadratic in k. Now Discriminant >=or <0 We get only a perfect square So Discriminant is always >=0 So k is always real

We will plot graphs of the function $f(x) = (x - t_1)(x - t_3),$ and $g(x) = k (x - t_2 )(x - t_4)$ for different values of $k$ . Both of them will be parabolæ (if $k \neq 0$ ); we can definitely say that $f(x)$ will open upwards because the coefficient of $x^2$ is positive, but the orientation of $g(x)$ will depend on $k$ .

Let $h(x) = f(x) + g(x)$ . We are to determine the nature of roots of $h(x)$ . The intervals for $k$ are chosen in such a way that in any interval, the sign of the coefficients of $x^2$ of $g$ and $h$ do not change in an interval.

Case 1. $k > 0$

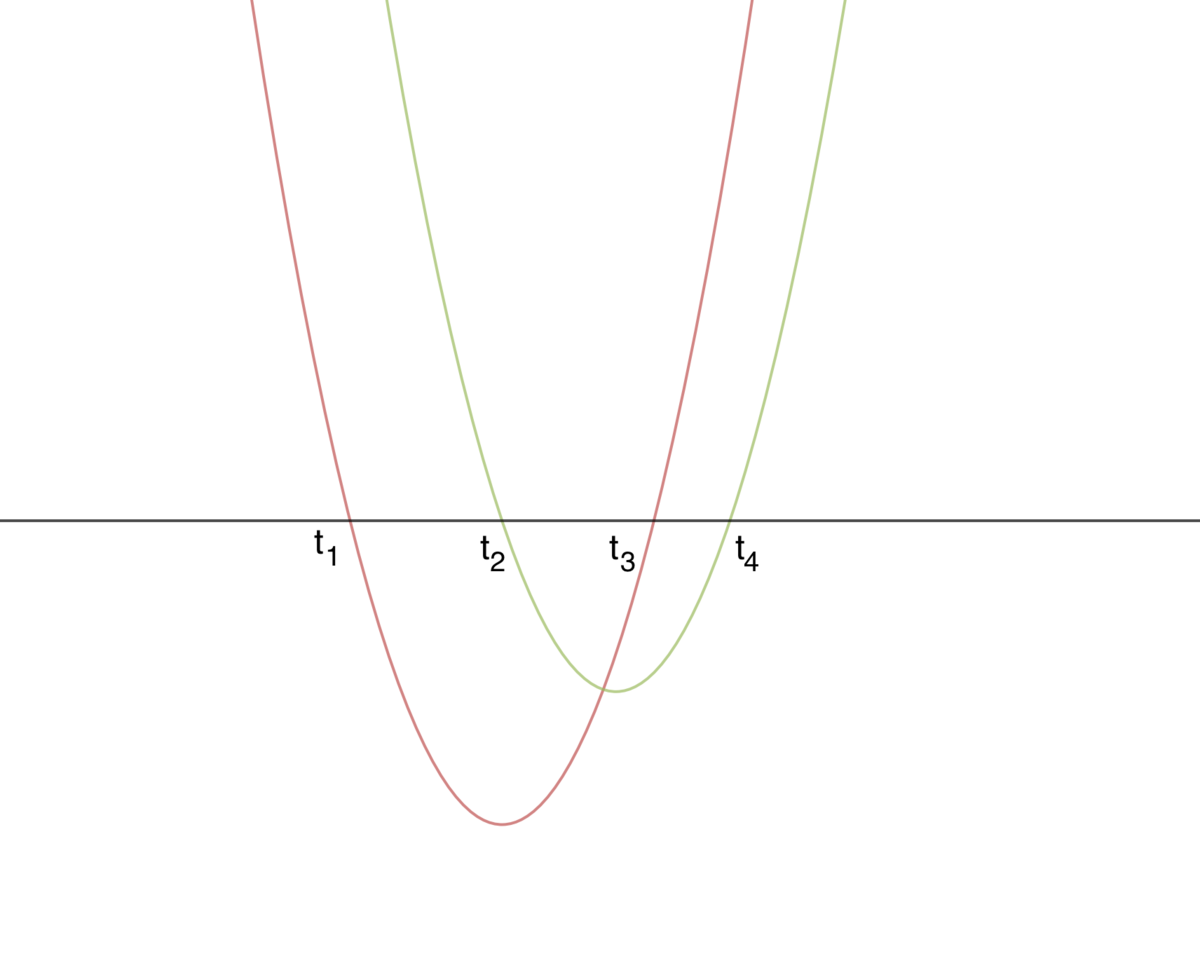( $f$ is plotted in red, $g$ is plotted in green)

$g$ will also open upwards. When we plot $h$ , it will also be a upwards opening parabola. Since $f$ and $g$ are both negative in the interval $(t_2, t_3)$ , $h$ will definitely be negative in this interval. It means $h$ crosses the $x$ - axis twice, and therefore $h(x) = 0$ has real roots.

Case 2. $k =0$

When $k = 0$ , $g(x) = 0$ , therefore $h(x) = f(x)$ . $f$ has two real roots $t_1$ and $t_3$ , so $h$ also has real roots.

Case 3. $-1 < k < 0$

The coefficient of $x^2$ in $h$ is positive, so $h$ will be upward opening parabola. The graph of $f$ and $g$ will look like this.

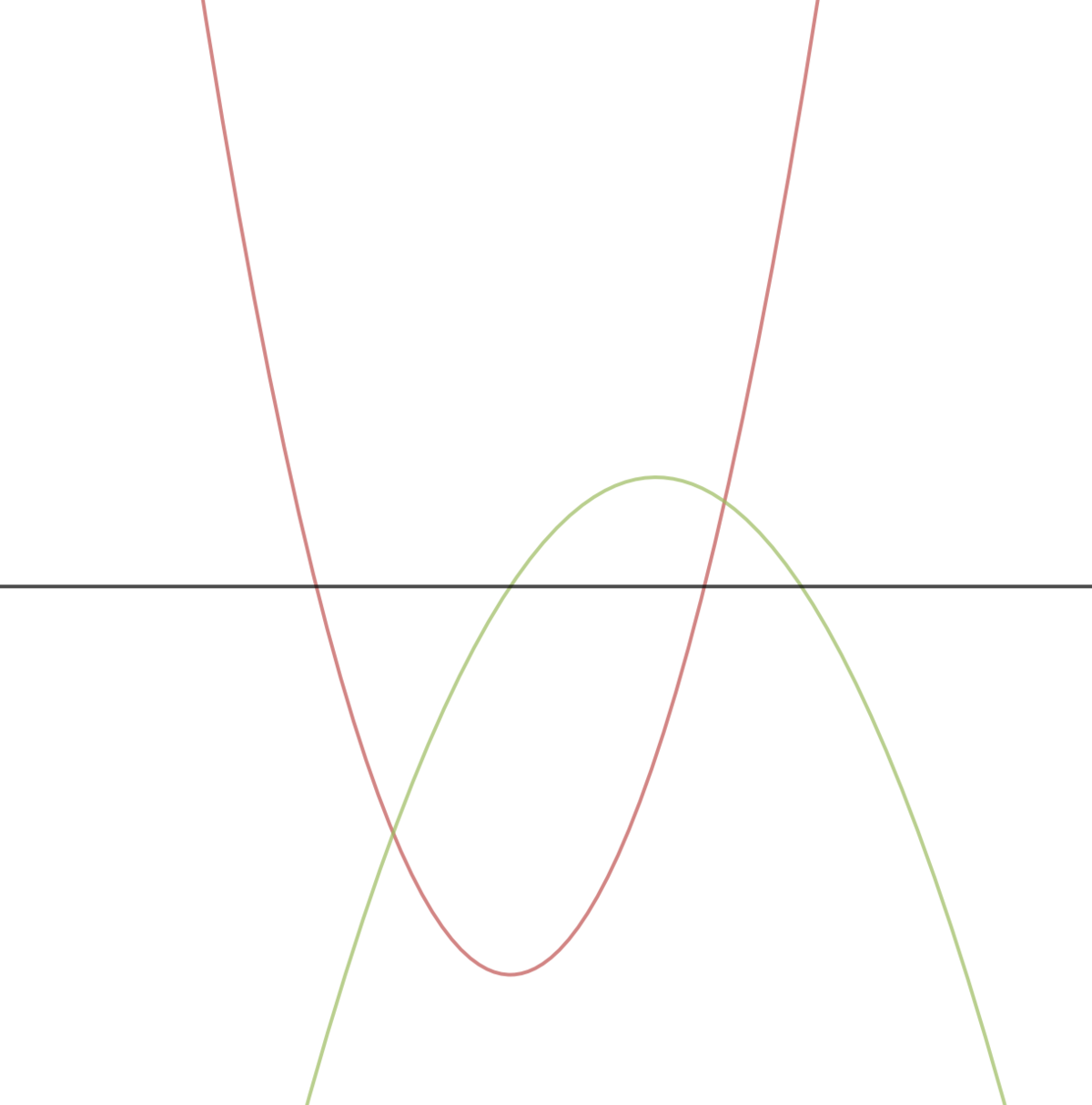
Since there exists an interval (between $t_1$ and $t_2$ ) where both $f$ \and $g$ are negative, there exists an interval where $h$ is negative; it crosses the $x$ axis twice and has two real roots.

Case 4. $k = -1$

The coefficient of $x^2$ is $0$ but coefficient of $x$ is not $0$ (because $t_1 + t_3 \neq t_2 + t_4)$ . $h$ is now linear with slope not zero, so it will definitely have a real root.

Case 5. $k < -1$

The coefficient of $x^2$ in $h$ is negative, so $h$ will be downward opening parabola. The graph of $f$ and $g$ will look like this.

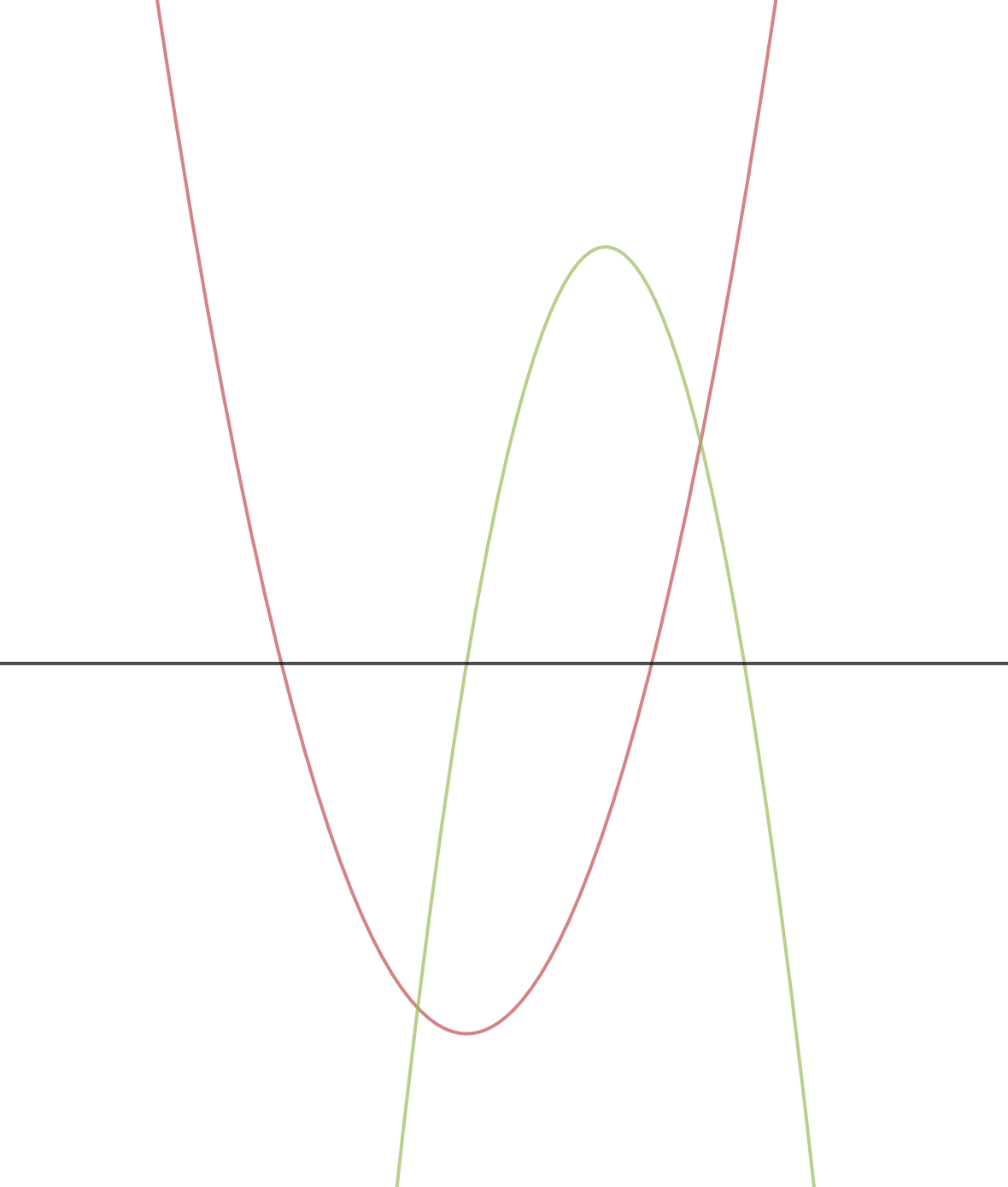
Since there exists an interval (between $t_2$ and $t_3$ ) where both $f$ and $g$ are positive, there exists an interval where $h$ is positive; it crosses the $x$ axis twice and has two real roots.

We have covered the entire real axis, and $h$ possesses real roots for every real value of $k$ . $_\square$

[(x-t1)(x-t3)]/[(x-t2)(x-t4)]=-k (By rearranging given equation)

[(x-t1)(x-t3)]/[(x-t2)(x-t4)]=0 Now of we plot this graph we would see that for any line parallel to x axis we will find atleast one point of intersection between graph and line this is sufficient to prove that for any value of k there would be atleast one real solution. P.S. somebody kindly upload graph for better visualization because i am unable to do so

Let $f(x) = (x-t_1)(x-t_3)+k(x-t_2)(x-t_4)$

We have:

$\begin{matrix} f(t_2) & = & (t_2-t_1)(t_2-t_3) & < & 0 \\ f(t_4) & = & (t_4-t_1)(t_4-t_3) & > & 0 \end{matrix}$

by the intermediate value theorem, it exists $\alpha$ in $(t_2,t_4)$ such $f(\alpha) = 0$