These sorts of geometry problems are pretty popular...
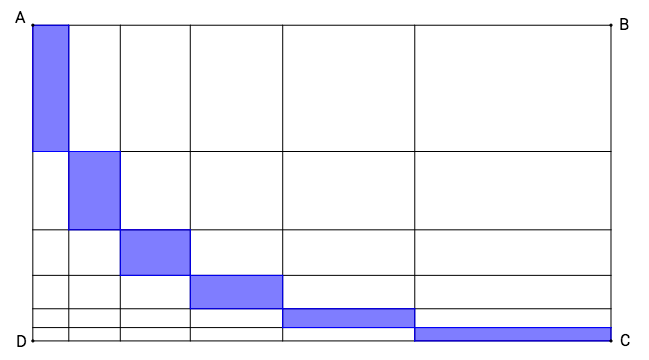
Rectangle is divided into 36 smaller rectangles by 5 horizontal segments and 5 vertical segments, as shown in the diagram.
The horizontal segments divide and in such a way that the lengths of the sub-segments of going from top to bottom are non-increasing.
The vertical segments divide and in such a way that the lengths of the sub-segments of going from left to right are non-decreasing.
Which region has a greater area: the region shaded in blue, or of ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First, a confession. The main focus of this problem isn't geometry. It's actually algebra! Let me explain why:
Let's let a 1 , a 2 , … , a 6 represent the lengths of the smaller segments of A D going from top to bottom, and let b 1 , b 2 , … , b 6 represent the lengths of the smaller segments of A B going from right to left. From the problem statement, we know that a i + 1 ≥ a i and b i + 1 ≥ b i for i = 1 , 2 , 3 , 4 , 5 .
By Chebyshev's Sum Inequality ,
6 1 ( i = 1 ∑ 6 a i ) ( i = 1 ∑ 6 b i ) ≥ i = 1 ∑ 6 a i b 7 − i .
However, notice that the right hand side of this inequality is actually the area of the blue region, which is a 1 b 6 + a 2 b 5 + ⋯ + a 6 b 1 . Furthermore, since i = 1 ∑ 6 a i = A D and i = 1 ∑ 6 b i = A B , the left hand side of the inequality is equal to 6 1 of the area of A B C D .
This leads us to conclude that the blue region has at most as much area as one-sixth of A B C D . Since one-fifth of A B C D has strictly greater area than one-sixth of A B C D , we conclude that 5 1 of A B C D always has a greater area than the blue region, no matter how we partition A B C D according to the given rules.