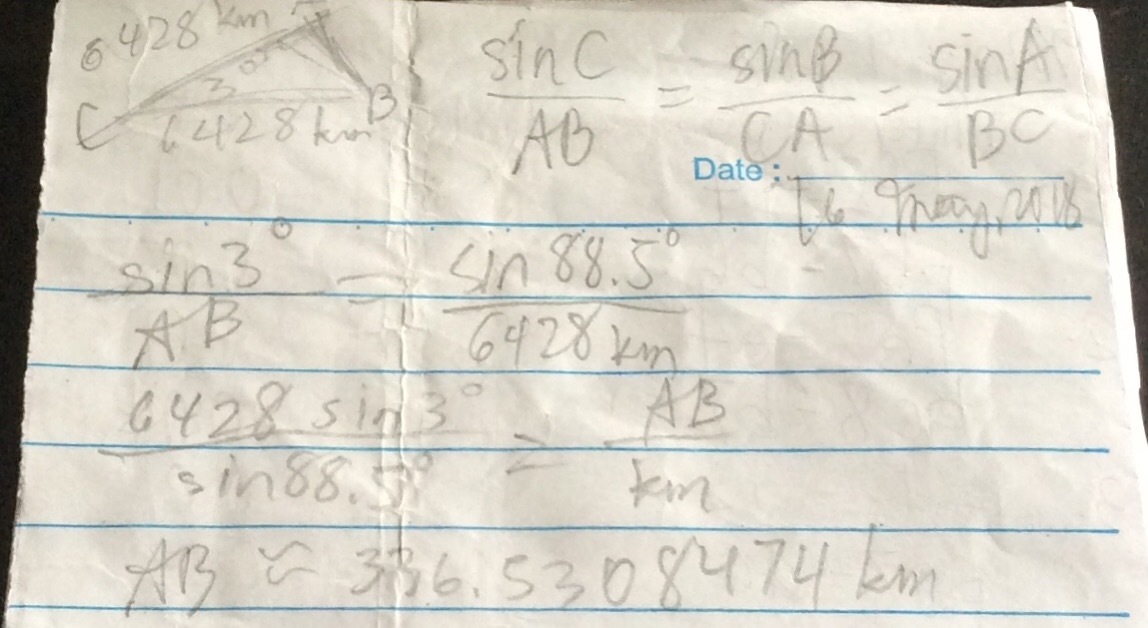Given that the radius of earth is 6428 km. A and B creates a angle in centre of earth.
Find the distance between A and B to 2 decimal places.(In km).
The answer is 336.57.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
See Sine Rule
Sine Law (Trigonometry)
Note: The author of the problem didn’t make clear that points A and B are points on the sphere... but here I’ll present my solution to this problem with an added condition that A and B are points on the sphere... until this condition has been incorporated into it, this solution will not be appropriate with the given conditions stated in the problem.
Name the center point O .
According to the problem, the length of the radius of the given sphere (assuming earth is a perfect sphere for the sake of the problem) is 6428 km. The problem also states that points
⇒ m ∠ A O B = 3 ° .
By law of sines, the lengths of the sides and the measures of the angles in a triangle X Y Z can be put into this relationship:
Connect the center O and points A and B together to form triangle AOB. (Definition of a triangle)
Assuming that A and B are points on the sphere, we have:
Thus, by definition of congruent segments, the length of O A is equal to the length of O B .
⇒ O A = O B = 6 4 2 8 k m . (From given that the radius measures 6428 km) Also, triangle O A B is an isosceles triangle since O A is congruent to O B . (Definition of an isosceles triangle)
⇒ ∠ B A O is congruent to ∠ O B A .
⇒ m ∠ B A O = m ∠ O B A (Definition of congruent angles: If angle P is congruent to angle S, then their measurements are equal.)
The sum of the measurements of all angles in a triangle is 180°. In the formed triangle here named AOB, m ∠ A O B + m ∠ B A O + m ∠ O B A = 1 8 0 ° .
Since m ∠ B A O = m ∠ O B A and m ∠ A O B = 3 ° , by substitution, we have:
By Addition Property of Equality (APE), add − 3 ° to both the LHS (left-hand side) and RHS (right-hand side) of the equation.
By MPE:
The distance from A to B is desired, therefore the value of A B is to be solved here. Applying sine law on triangle AOB, we have:
s i n ( m ∠ A O B ) A B = s i n ( m ∠ O B A ) O A .
Applying substitution of known values,
⇒ s i n ( 3 ° ) A B = s i n ( 8 8 . 5 ° ) 6 4 2 8 k m .
Applying MPE:
⇒ A B = s i n ( 8 8 . 5 ° ) 6 4 2 8 s i n ( 3 ° ) k m .
⇒ A B is around 3 3 6 . 5 3 0 8 4 7 4 k m . (Approximate answer using calculator.)
Rounded to two decimal places, the answer is 3 3 6 . 5 3 k m .
———
Another way, in a picture: