Thevenin/Norton Resistance
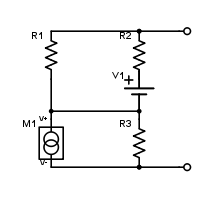
The elements of the linear circuit shown above have the following values:
- Resistors: , and
- Independent voltage sources:
- Independent current sources:
Calculate the Thevenin equivalent resistance (in ) between the circular nodes. Round off your answer to three decimal places.
The answer is 4.256.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
To calculate the Thevenin/Norton equivalent resistance, we "switch off" all independent sources (i.e. replace all voltage sources with a short circuit and replace all current sources with an open circuit) then calculate the resistance seen from the port.
With all independent sources set to zero, we are left with the following network: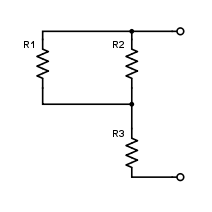 Between the two nodes, the resistance is
R
1
∣
∣
R
2
+
R
3
=
4
.
2
5
5
9
3
2
2
0
3
3
8
9
8
3
.
.
.
Between the two nodes, the resistance is
R
1
∣
∣
R
2
+
R
3
=
4
.
2
5
5
9
3
2
2
0
3
3
8
9
8
3
.
.
.