They are so many
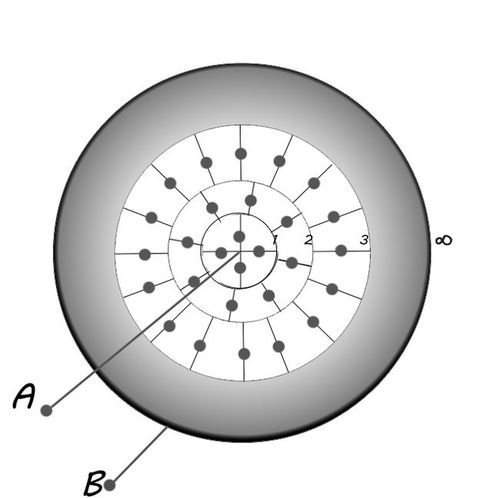 In the image above, gray dots are capacitors of capacitance
1
μ
f
.
In the image above, gray dots are capacitors of capacitance
1
μ
f
.
That gray area shows that, there is infinite arrangement of capacitors, such that first circle has 4 capacitors , second one has 8 capacitors, third 16 capacitors and next 32 and so on, as shown.
Find the equivalent capacitance in μ f between the two terminals A (at the center) and B (at infinity).
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
~ 4 C ~ 8 C ~ 16 C ~ 32 C ~ ... (in series to infinite terms.):
4 1 + 8 1 + 1 6 1 + 3 2 1 + 6 4 1 + . . . 1 = 2
OR step by step using C s e r i e s c a p a c i t a n c e = C 1 + C 2 C 1 C 2 :
1 2 3 4 5 6 7 8 9 10 |
|
Answer: 2
JUST A SUM OF GEOMETRIC PROGRESSION 4,8,........... AS THE CAPACITORS OR IN PARALLEL CONNECTION .
We can see that as we go outwards from pt a to b the first 4 capacitors appear to be in parallel then the next 8 appear to be in parallel this is because each circle is an equipotential surface , the system of the first four capacitors is in series with the system of the next 8 and so on till infinity.
Thus , 1/c = (1/4 (1))/ (1-1/2) using sum of infinite gp c= 2