They call it chemical kinetics?
The Arrhenius equation above tell us how the rate constant for a particular reaction depends on its activation energy and temperature
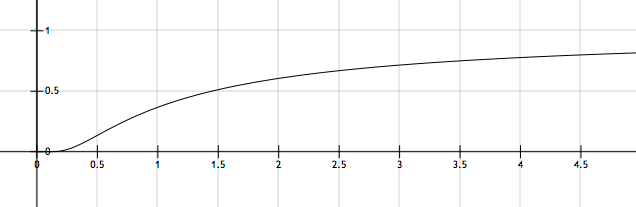
The figure above shows a typical plot of versus . If the corresponding value of for the point of inflection for the curve above is given by for some constant then find
Assumptions and Clarifications:
- The pre-exponential factor or for the given reaction is essentially a constant.
- is the gas constant.
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Firstly, we need to determine what the values of A and E A are. We can do this by estimating two points on the given graph - I'll choose ( 0 . 7 5 , 0 . 2 5 ) and ( 1 . 5 , 0 . 5 ) (I have omitted units to make the calculations more readable). Since A and E A are constant regardless of our choice of T , we can write:
e − 0 . 7 5 K ∗ R E A 0 . 2 5 = e − 1 . 5 ∗ R E A 0 . 5
Which, through simplification, gives us:
e R E A ( 0 . 7 5 1 − 1 . 5 1 ) = 2
Meaning that E A = 2 3 R ln ( 2 ) and A = 0 . 2 5 e 0 . 7 5 R E A = 1
Now we need to determine the formula for the inflection point of k ( T ) . We have k ( T ) = A e − R T E A meaning that k ′ ( T ) = R T 2 E A A e − R T E A and k ′ ′ ( T ) = − R T 3 2 E A A e − R T E A + R 2 T 4 E A 2 A e − R T E A We can vastly simplify k ′ ′ ( T ) by factoring out R E A A e − R T E A , giving us k ′ ′ ( T ) = R E A A e − R T E A ( − T 3 2 + R T 4 E A ) . To find the inflection point of k ( T ) , we need to find a T such that k ′ ′ ( T ) = 0 . This can only happen if − T 3 2 + R T 4 E A = 0 and since the T we want will be positive, we can multiply this expression by T 3 to give us − 2 + R T E A = 0 . There is therefore an inflection point at T = 2 R E A = 4 3 ln ( 2 ) K
The value of k at this inflection point is k ′ = A e − R T E A = A e − 2 . Finally, we conclude that ∣ X ∣ = 2