They call it logarithms?

Let us consider $2$ cases,

Case $1:$

$\underbrace{0<\frac{3x}{x^2+1}<1}_{ x\in \left(0,\frac{3-\sqrt{5}}{2}\right) \cup \left( \frac{3+\sqrt{5}}{2},\infty \right)}$

Keeping the above range of acceptable $x$ in mind and solving,

$\log_{\frac{3x}{x^2+1}} \left(x^2-\frac{5}{2}x+1\right) \geq 0 \\ 0<x^2-\frac{5}{2}x+1≤1 \\ x\in \left( 0 , \frac{3-\sqrt{5}}{2}\right)$

Case $2:$

$\underbrace{\frac{3x}{x^2+1}>1}_{ x\in \left(\frac{3-\sqrt{5}}{2}, \frac{3+\sqrt{5}}{2} \right) }$

Keeping the above range of acceptable $x$ in mind and solving,

$\log_{\frac{3x}{x^2+1}} \left(x^2-\frac{5}{2}x+1\right) \geq 0 \\ x^2-\frac{5}{2}x+1≥1 \\ x\in \left[\frac{5}{2},\frac{3+\sqrt{5}}{2}\right)$

Therefore,

$x\in \left( 0 , \frac{3-\sqrt{5}}{2}\right) \cup \left[\frac{5}{2},\frac{3+\sqrt{5}}{2}\right) \\ \Rightarrow a+b+c+d =0+\frac{3-\sqrt{5}}{2}+\frac{5}{2}+\frac{3+\sqrt{5}}{2}=\frac{11}{2}=\boxed{5.5}$

Here we can do a change of base, let´s put all the expression with a base of 10:

$\log _{ \frac { 3x }{ { x }^{ 2 }+1 } }{ ({ x }^{ 2 }-\frac { 5 }{ 2 } x+1) }\ge 0=$ $\frac { \log { { (x }^{ 2 }-\frac { 5 }{ 2 } x+1) } }{ \log { (\frac { 3x }{ { x }^{ 2 }+1 } ) } }\ge 0$

1st: Domain of the function

Now we have to consider the domains of both logarithms to know when the function has real values:

$\frac{3x}{x^2+1}$ $>0$ , solving this inequality the domain of the logarithm is $x\in (0,\infty )$ . However, this is the domain if this logarithm wouldn´t be in the denominator, so we have to calculate the values where the function equals zero because these values make the fraction undefined:

$\log { \frac { 3x }{ { x }^{ 2 }+1 } \neq 0 }$ , this equals to $x\neq \frac { 3\pm \sqrt { 5 } }{ 2 }$ , note that both numbers are positive, so they change the domain.

With this, the domain of the denominator is $x\in (0,\infty )\quad for\quad x\neq \frac { 3\pm \sqrt { 5 } }{ 2 }$

${ x }^{ 2 }-\frac { 5 }{ 2 } x+1>0$ , solving this inequality the domain of the logarithm (numerator) is $x\in (-\infty ,\frac { 1 }{ 2 } )\cup (2,\infty )$ .

Now, the domain of the fraction equals the intersection of the domains above:

${ Dom }_{ Num }\cap { Dom }_{ Den }=\quad x\in (0,\frac { 3-\sqrt { 5 } }{ 2 } )\cup (\frac { 3-\sqrt { 5 } }{ 2 } ,\frac { 1 }{ 2 } )\cup (2,\frac { 3+\sqrt { 5 } }{ 2 } )\cup (\frac { 3+\sqrt { 5 } }{ 2 } ,\infty )$ .

2nd: The roots

We calculate the roots of the numerator and the denominator to solve this inequality (see step 3). We know the roots of the denominator, so let´s calculate the roots of the numerator:

$\log { ({ x }^{ 2 }-\frac { 5 }{ 2 } x+1) } =0\rightarrow { x }^{ 2 }-\frac { 5 }{ 2 } x+1=1\rightarrow x(x-\frac { 5 }{ 2 } )=0$ . With this $x=\left\{ 0,\frac { 5 }{ 2 } \right\}$

3rd: Solutions

For this case, let $\circ$ the open interval for the set of solutions and $\bullet$ be the close interval for the set of solutions. So, in this case, we are going to evaluate the function in values between the roots (either the numerator or the denominator) to determine when this is positive or negative in this way:

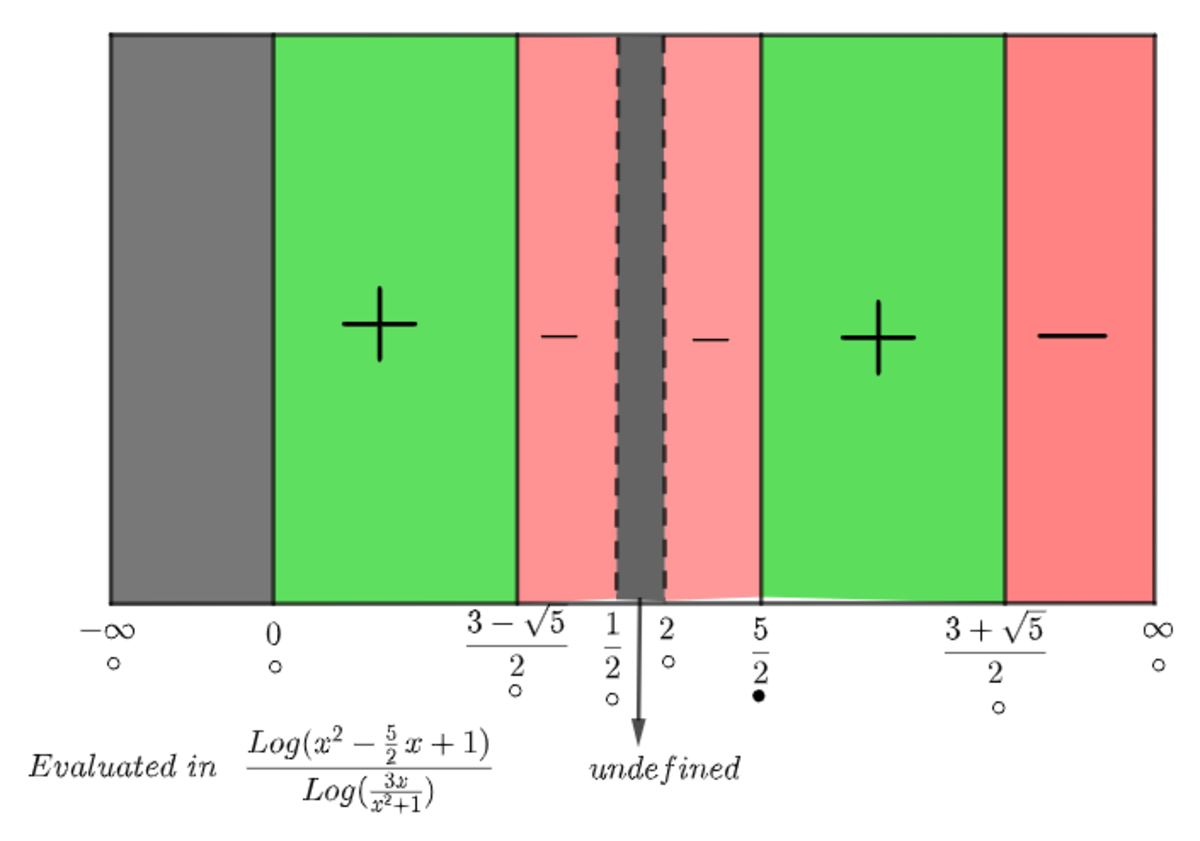
According to this, the solution to this inequality is $x\in (0,\frac { 3-\sqrt { 5 } }{ 2 } )\cup [\frac { 5 }{ 2 } ,\frac { 3+\sqrt { 5 } }{ 2 } )$

Finally, the sum of these coefficients equals to

$a+b+c+d=\frac { 3+3+5+\sqrt { 5 } -\sqrt { 5 } +0 }{ 2 } =\frac { 11 }{ 2 } =5.5$