They Look Like Pythagorean Triple
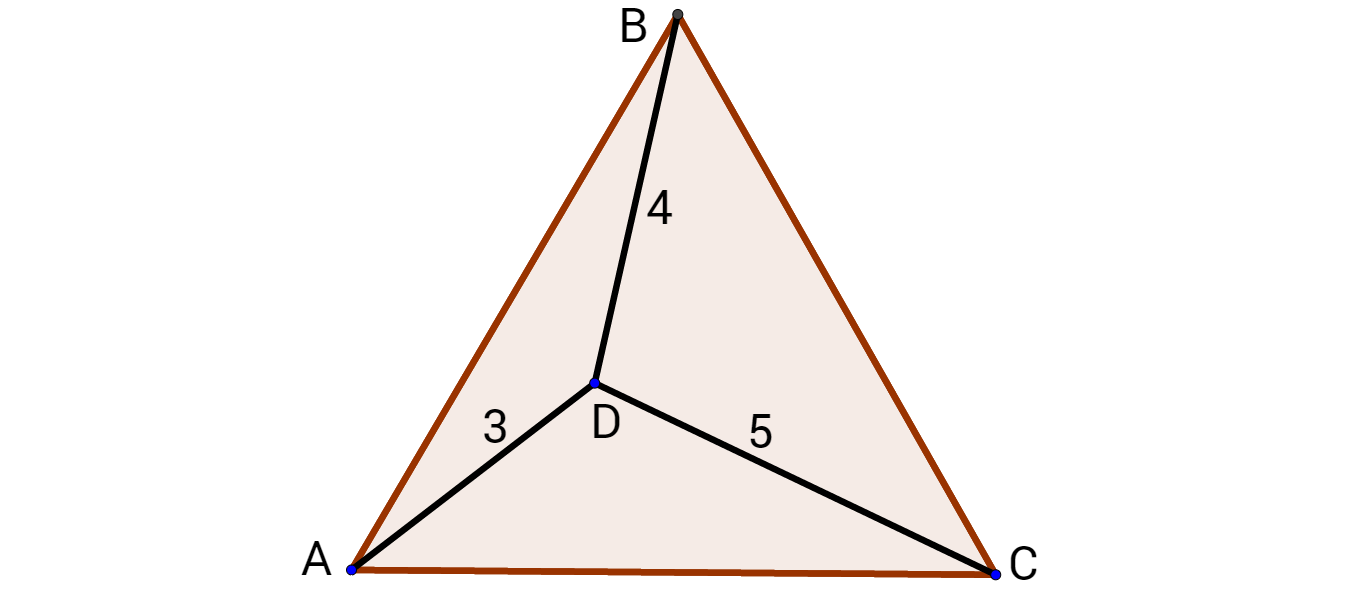 Triangle
A
B
C
above is an equilateral triangle and
A
D
=
3
,
B
D
=
4
and
C
D
=
5
. Find
A
B
.
Triangle
A
B
C
above is an equilateral triangle and
A
D
=
3
,
B
D
=
4
and
C
D
=
5
. Find
A
B
.
The answer is 6.76643.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Nice solution.
Amazing solution.
link text
In an equivalent triangle side S, if a point inside it is at distances X, Y, Z from the vertices, their relation is given in the link above by,
3
(
X
4
+
Y
4
+
Z
4
+
S
4
)
=
(
X
2
+
Y
2
+
Z
2
+
S
2
)
2
⟹
3
(
3
4
+
4
4
+
5
4
+
S
4
)
=
(
3
2
+
4
2
+
5
2
+
S
2
)
2
.
E
x
p
a
n
d
i
n
g
a
n
d
s
i
m
p
l
i
f
y
i
n
g
,
2
S
2
−
1
0
0
S
+
3
8
6
=
0
o
r
S
2
−
5
0
S
+
1
9
3
=
0
.
S
o
l
v
i
n
g
t
h
e
q
u
a
d
r
a
t
i
c
S
2
=
4
5
.
7
8
4
6
,
r
e
j
e
c
t
i
n
g
t
h
e
o
t
h
e
r
r
o
o
t
b
e
i
n
g
t
o
o
s
m
a
l
l
.
∴
S
=
6
.
7
6
6
4
3
2
5
Nice, I did not know the result. Thanks for sharing your solution
Refer here to get that twice the area of the equilateral triangle is 2 5 2 3 + 1 8 Hence, if the side of the required triangle is a , a 2 2 3 = 2 5 2 3 + 1 8 ⟹ a = 2 5 + 1 2 3 ≈ 6 . 7 6 6
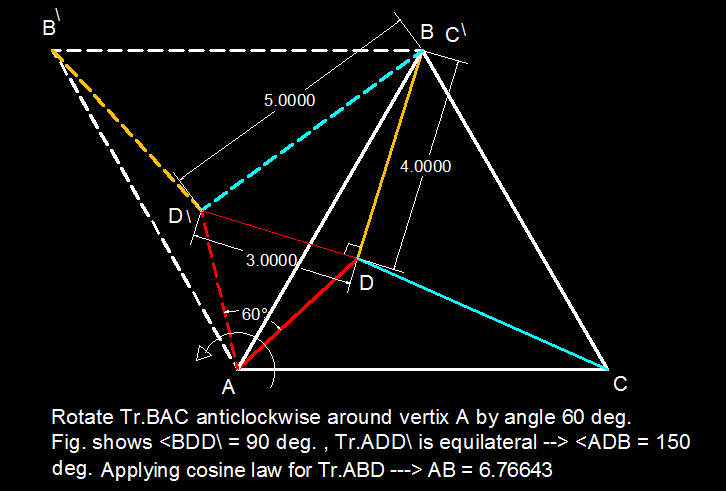
 Rotate triangle
A
B
C
in magnitude of
6
0
∘
in the counterclockwise direction as shown in my figure.
Rotate triangle
A
B
C
in magnitude of
6
0
∘
in the counterclockwise direction as shown in my figure.
sin ∠ D ’ D C = 5 3
∠ D ’ D C ≈ 3 6 . 8 7 ∘
By cosine rule, we have
( B C ) 2 = 4 2 + 5 2 − 2 ( 4 ) ( 5 ) [ cos ( 6 0 + 3 6 . 8 7 ) ]
B C = A B ≈ 6 . 7 6 6 units
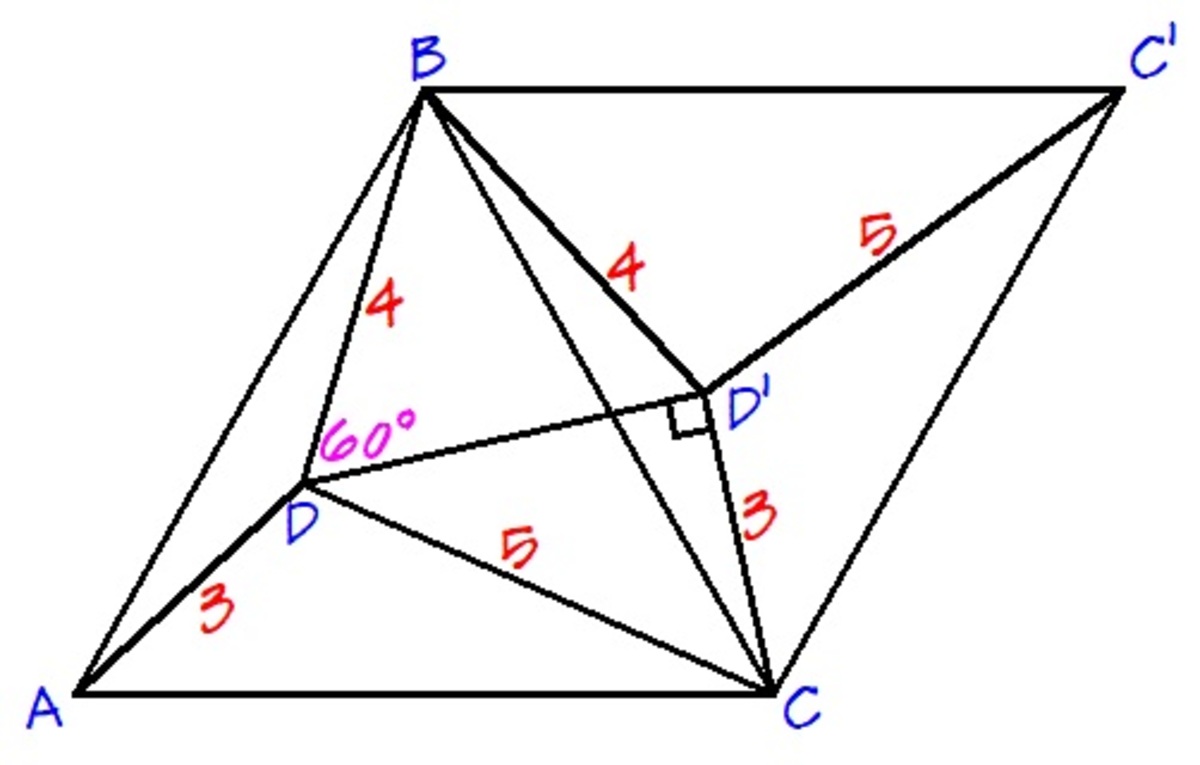
Let generalize this problem for any Pythagorean triple with cathetus a and b , and hypotenuse c .
First moves △ A P C together △ A P B as image shows, clearly, △ A P ′ P is an equilateral triangle and △ P P ′ B is an rectangle triangle of sides a , b and c so ∠ B P A = 6 0 ° + 9 0 ° = 1 5 0 ° .
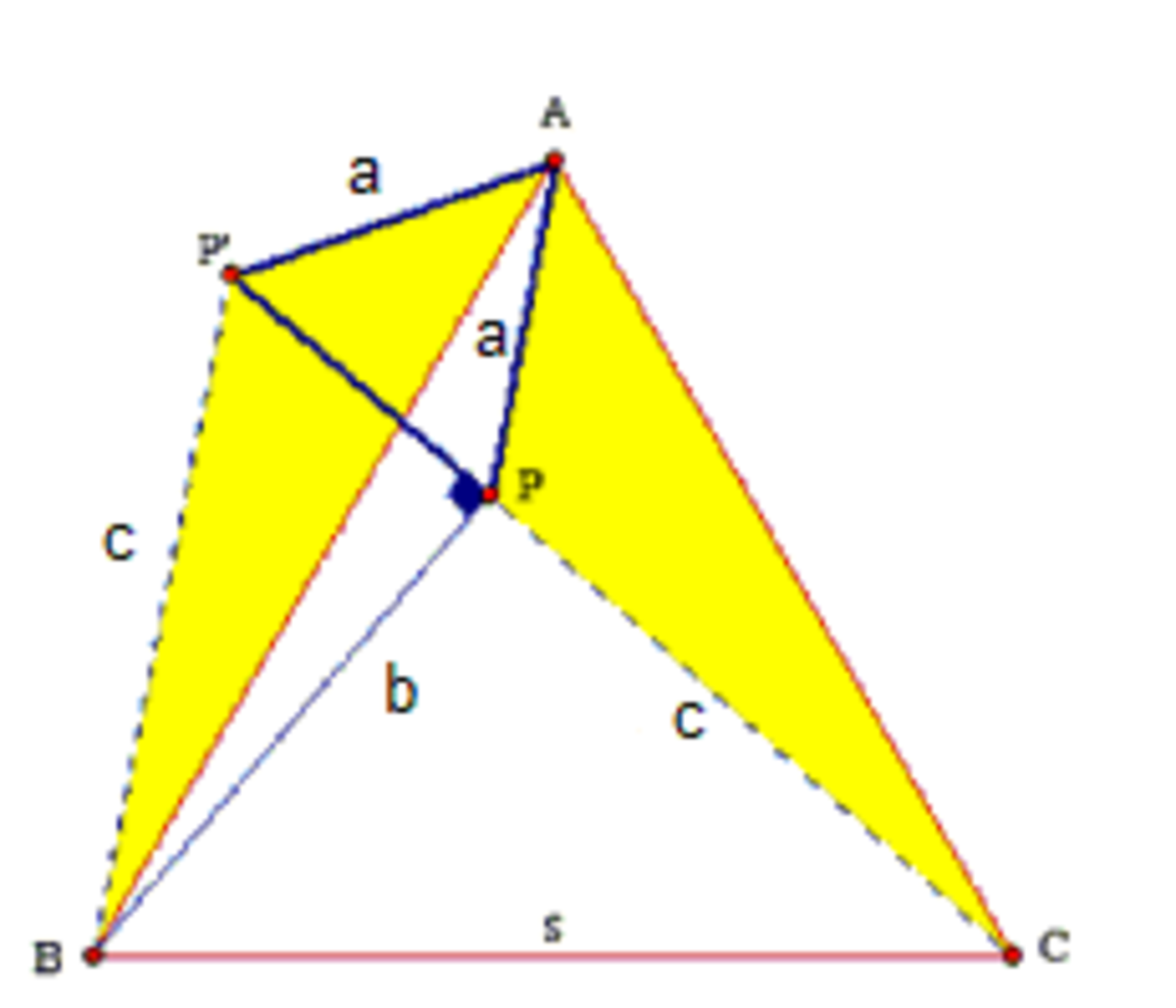
By law of cosines, the side of the equilateral triangle is s = a 2 + b 2 − 2 ( a ) ( b ) cos 1 5 0 ° .
For this triangle A B = 3 2 + 4 2 − 2 ( 3 ) ( 4 ) cos 1 5 0 ° ≈ 6 . 7 6 6 .
Similar problem: Equilateral triangle point
Any question, be free of asking in comments.