Think about a triangle
⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ a 2 + a b + b 2 b 2 + b c + c 2 c 2 + c a + a 2 = 2 5 = 4 9 = 6 4
a , b , c are positive reals that satisfy the system of equations above.
Find the value of ( a + b + c ) 2 .
The answer is 129.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Squaring the the equation c − a 8 = a − b 5 was an excellent idea! Nice solution!
Please explain the cross multiplying step
Log in to reply
6 4 − 3 a c 6 4 = 2 5 − 3 a b 2 5 ⟹ 6 4 ⋅ 2 5 − 6 4 ⋅ 3 a b = 2 5 ⋅ 6 4 − 2 5 ⋅ 3 a c ⟹ 6 4 ⋅ 3 a b = 2 5 ⋅ 3 a c ⟹ 6 4 b = 2 5 c
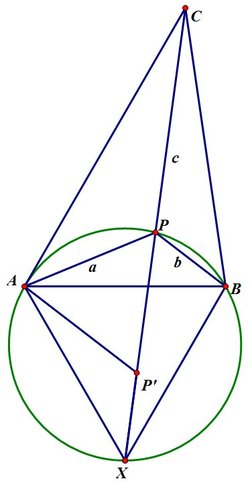 Consider a triangle
A
B
C
with sides
A
B
=
5
,
B
C
=
7
,
A
C
=
8
, and let
P
be the Steiner point inside the triangle which subtends an angle of
1
2
0
∘
with each pair of the points
A
,
B
,
C
. Note that
P
can be constructed by constructing the equilateral triangle
A
B
X
, in which case
P
is the point of intersection (other than
X
) of the line
C
X
with the circumcircle of
A
B
X
. Suppose that
a
=
A
P
,
b
=
B
P
and
c
=
C
P
. Applying the Cosine Rule to each of the triangles
A
B
P
,
B
C
P
,
A
C
P
shows that
a
,
b
,
c
satisfy the desired identities.
Consider a triangle
A
B
C
with sides
A
B
=
5
,
B
C
=
7
,
A
C
=
8
, and let
P
be the Steiner point inside the triangle which subtends an angle of
1
2
0
∘
with each pair of the points
A
,
B
,
C
. Note that
P
can be constructed by constructing the equilateral triangle
A
B
X
, in which case
P
is the point of intersection (other than
X
) of the line
C
X
with the circumcircle of
A
B
X
. Suppose that
a
=
A
P
,
b
=
B
P
and
c
=
C
P
. Applying the Cosine Rule to each of the triangles
A
B
P
,
B
C
P
,
A
C
P
shows that
a
,
b
,
c
satisfy the desired identities.
Rotate the triangle A B P through 6 0 ∘ clockwise about the point A to form the triangle A X P ′ . Note that P ′ lies on the line X C . Then A P P ′ is equilateral, and it is clear that a + b + c = A P + B P + C P = P P ′ + P ′ X + C P = C X
Set up a coordinate system so that A has coordinates ( 0 , 0 ) and B has coordinates ( 5 , 0 ) . Then X has coordinates ( 2 5 , − 2 5 3 ) . Using the Cosine rule on the triangle A B C , we see that ∠ C A B = 6 0 ∘ , and so C has coordinates ( 4 , 4 3 ) . Thus ( a + b + c ) 2 = C X 2 = ( 2 3 ) 2 + ( 2 1 3 3 ) 2 = 1 2 9 . Alternatively, we could apply the Cosine Rule to the triangle C A X , with ∠ C A X = 1 2 0 ∘ , to show that C X 2 = 1 2 9 .
Extra ordinary solution.
Can you explain what the steiner point means?
Log in to reply
It is the point P that subtends an angle of 1 2 0 ∘ with each pair of the vertices A , B , C . It is also the point that minimizes the sum P A + P B + P C of the distances to the vertices. For a triangle such as this, it is also known as the first Fermat point of the triangle.
As elegant as this solution seems, it is quite time consuming and will require a graph, assuming we are obtaining a hand written solution.
Log in to reply
Well, the construction of the Steiner point P is a matter of bookwork. I took the time to prove the bookwork here. Given the bookwork, it is only necessary to determine the coordinates of X and hence calculate the length C X .
The equations can be solved by purely algebraic means, of course, but that means that you do not get the geometric insight into what is going on here.
Rewriting the equations,
( a + b ) 2 − a b = 2 5
( b + c ) 2 − b c = 4 9
( a + c ) 2 − a c = 6 4
Now subtracting 1 from 2 , 2 from 3 , and 1 from 3 ,
( a + b + c ) ( c − a ) = 2 4
( a + b + c ) ( a − b ) = 1 5
( a + b + c ) ( c − b ) = 3 9
Hence, we have:
c − a 2 4 = a − b 1 5 = c − b 3 9 ⟹ c − a 8 = a − b 5 = c − b 1 3 ⟹ c − a 8 = a − b 5 ⟹ a 2 + c 2 − 2 a c 6 4 = a 2 + b 2 − 2 a b 2 5 ⟹ a 2 + c 2 + a c − 3 a c 6 4 = a 2 + b 2 + a b − 3 a b 2 5 ⟹ 6 4 − 3 a c 6 4 = 2 5 − 3 a b 2 5
Cross multipltying, we have 6 4 b = 2 5 c ⟹ c = 2 5 6 4 b
Substituting 2 5 6 4 b in (2), we have:
( b + 2 5 6 4 b ) 2 − 2 5 6 4 b 2 = 4 9 ⟹ b = 1 2 9 2 5 (b is a positive real)
c = 2 5 6 4 b = 2 5 6 4 ⋅ 1 2 9 2 5 = 1 2 9 6 4
Substituting c = 1 2 9 6 4 in (3), we have a = 1 2 9 4 0 (a is a positive real)
Hence, ( a + b + c ) 2 = ( 1 2 9 4 0 + 1 2 9 2 5 + 1 2 9 6 4 ) 2 = ( 1 2 9 1 2 9 ) 2 = 1 2 9