Think about the geometry
Find the minimum of 5 8 − 4 2 x + 1 4 9 − 1 4 0 1 − x 2 , where − 1 ≤ x ≤ 1 .
The minimum can be expressed as a , where a is a square-free integer. What is a ?
Source: 2017 HMNT #9, General Round
The answer is 109.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Log in to reply
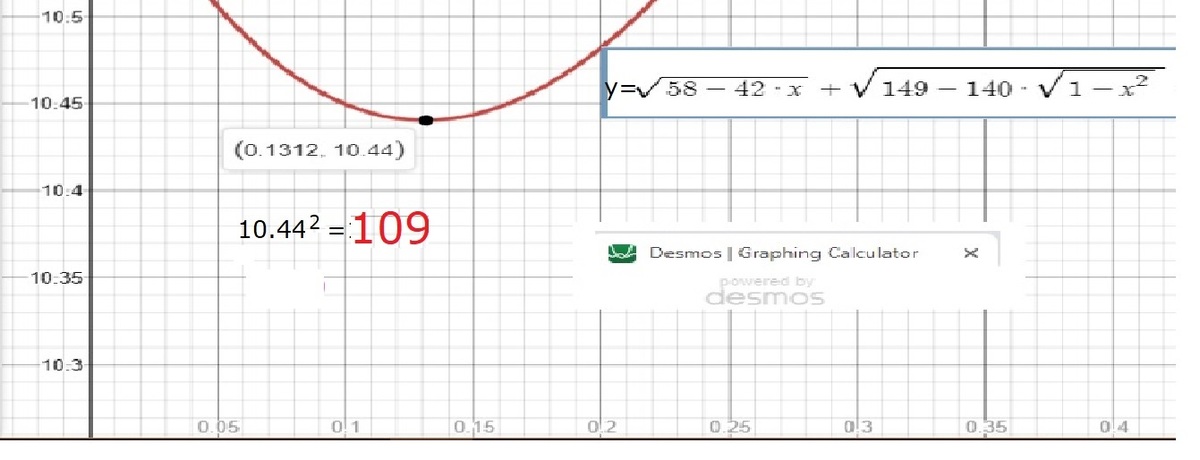
I tried to continue using half-angle formulas after your first step since the numbers looked nice though I couldn't get anything. What I mean is that 149-140 = 9 = 3^2, 149+140 = 289 = 17^2, 289 - 2 140 = 9 = 3^2, 58+42= 100 = 10^2, 58-42 = 16 = 4^2, 100 - 2 42 = 16 = 4^2. These were all things that I was trying to use to solve the problem.
 O
R
O
R
f
(
x
)
=
1
4
9
−
1
4
0
∗
1
−
x
2
+
5
8
−
4
2
∗
x
.
f
′
(
x
)
=
(
1
−
x
2
)
∗
1
4
9
−
1
4
0
∗
1
−
x
2
7
0
x
−
5
8
−
4
2
∗
x
2
1
=
0
.
U
s
i
n
g
"
k
i
s
s
a
n
o
n
l
i
n
e
A
d
v
a
n
c
e
d
C
a
l
c
u
l
a
t
o
r
"
:
−
−
1
,
.
1
,
2
0
,
g
a
v
e
l
o
w
e
s
t
b
e
t
w
e
e
n
.
0
a
n
d
.
2
.
0
,
.
0
1
,
2
0
,
g
a
v
e
l
o
w
e
s
t
b
e
t
w
e
e
n
.
1
2
a
n
d
.
1
4
.
.
1
2
,
.
0
0
1
,
2
0
,
g
a
v
e
l
o
w
e
s
t
b
e
t
w
e
e
n
.
1
3
a
n
d
1
5
.
a
n
d
s
o
o
n
,
I
g
o
t
u
p
t
o
x
=
0
.
1
3
1
1
6
3
1
9
1
.
f
(
0
.
1
3
1
1
6
3
1
9
1
)
=
1
0
9
=
a
⟹
a
=
1
0
9
.
Only the blue portion is my input. Why there is extra black portion below OR!!!!
You can't do anything by your own
Note that the quantity can suspiciously be written as 7 2 + 3 2 − 2 ( 7 ) ( 3 ) x + 1 0 2 + 7 2 − 2 ( 7 ) ( 1 0 ) 1 − x 2 . The quantities under the radical remind us of the law of cosines, so let's make the substitution x = cos ( α ) and thus 1 − x 2 = sin ( α ) = cos ( π / 2 − α ) , taking care to note that we are now optimizing over 0 ≤ α ≤ π .
Our expression now looks like 7 2 + 3 2 − 2 ( 7 ) ( 3 ) cos ( α ) + 1 0 2 + 7 2 − 2 ( 7 ) ( 1 0 ) cos ( π / 2 − α ) .
Let c = 7 2 + 3 2 − 2 ( 7 ) ( 3 ) cos ( α ) and c ′ = 1 0 2 + 7 2 − 2 ( 7 ) ( 1 0 ) cos ( π / 2 − α ) . Geometrically, we have the triangles c − 7 − 3 and c ′ − 7 − 1 0 . Note that because they have a common side and because the angle opposite to c is α and the angle opposite to c ′ is π / 2 − α , we can put the two triangles together to obtain a quadrilateral with a right angle like in the following picture:
Clearly, c + c ′ is minimized when c and c ′ form the hypotenuse of the right triangle with sides 3 and 1 0 , so the minimal value is 1 0 9 .