Think about two folds
In △ A B C , B E is a median and O is the midpoint of B E . The line joining A and O meets B C at D . Find the ratio of the lengths A O : O D .
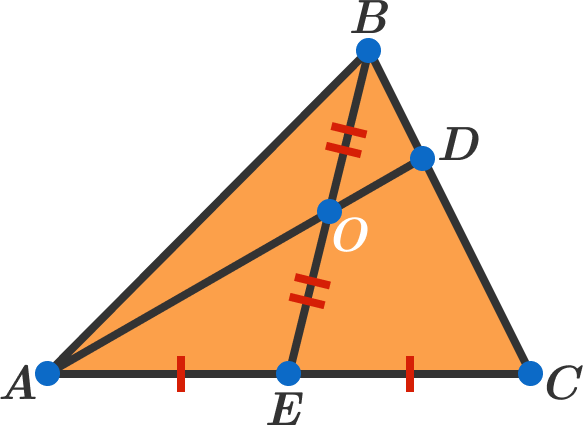
The answer is 3.000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Add D , E
Now let Δ A B E = x and Δ B D O = a
So Δ A B E = Δ B E C = x
So Δ B D O = Δ D E O = a
Then Δ A D E = Δ D E C = x + a
So Δ B E C = x + 3 a = 2 x
Then a = x / 3
So A O : O D = x : a = 1 : 1 / 3 = 3 : 1
Using Menelaus's Theorem in Δ BEC with transversal AD ,
E A C A × B O E O × D C B D = 1
Using the given conditions this simplifies to DC = 2 BD , and similarly for Δ ACD with transversal BE we get,
B D C B × O A D O × E C A E = 1 B D B D + D C = O D A O O D A O = B D 3 B D = 3
Draw E F parallel to A D as shown.
It can be easily shown that Δ B O D and Δ B E F are similar triangles. Thus by the basic proportionality theorem, we have
⟹ ⟹ B E B O 2 1 E F = = = E F O D E F O D 2 O D
Also, Δ C E F and Δ C A D are similar. Thus by BPT,
⟹ ⟹ ⟹ ⟹ ⟹ C A C E 2 1 A D A O + O D A O O D A O = = = = = = A D E F A D E F 2 E F 4 O D 3 O D 1 3