A probability problem by Twisting Tiger
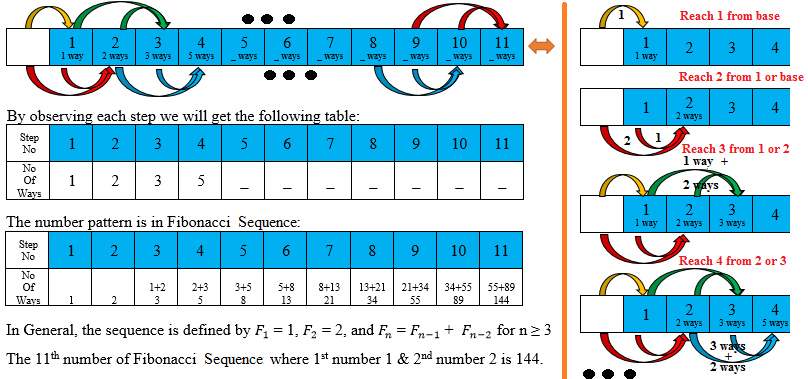
The diagram below shows stairs with eleven steps. Moving up only 1 or 2 steps at a time, how many different ways can a person reach the top?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
wolfram input: sum(C(n,2n-11)), n=6 to 11 // result = 144 // 2 2 2 2 2 1 // 2 2 2 2 1 1 1 // 2 2 2 1 1 1 1 1 // 2 2 1 1 1 1 1 1 1 // 2 1 1 1 1 1 1 1 1 1 // 1 1 1 1 1 1 1 1 1 1 1 // C(a,b) = Combinations = a! /(a-b)! b!
Well as a Chinese student I have to say that this problem is used as an exam problem of Tsinghua University. BUT itself is quite attractive.
Why did you divide?
Log in to reply
Because they are repeated steps, just like the last one, 0 (2 steps) and 11 (1 step) it doesnt mean that is equal to 11! Just because the 11 steps is repeated, therefore it should divide by 11
Log in to reply
Oops sry it should be divide by 11! Making that to be (11!/11! = 1) way to reach the top
Let S ( i ) denote the number of different ways to reach up to the i th step. Clearly, S ( 1 ) = 1 , S ( 2 ) = 2 . For i ≥ 3 , to reach the ith step, the last step may be of length 1 or 2 . Hence, S ( i ) = S ( i − 1 ) + S ( i − 2 ) Solving this recursion, we get the answer S ( 1 1 ) = 1 4 4 .
Moderator note:
There is a closed-form version of the Fibonacci sequence; specifically, letting ϕ = 2 1 + 5 be the golden ratio:
F n = 5 ϕ n − ( ϕ − 1 ) n .
A short proof by induction is here .
So it is just the Fibonacci numbers in disguise.Nice!
Why can't I go up and and down n times on step k mid way through my ascension of the flight overall? This surely gives an infinite variety of possibilities?
Log in to reply
The problem specifically states "moving up ". Down is not allowed.
Log in to reply
Ah, my bad. My physics teacher used to give the following exam advice, "if all else fails, read the question! "
I think I used the Binary notation to this one to solve how many 2-steps could be performed. 10010000 = 144 combination. Is this possible?!
Log in to reply
Perhaps you should write up your solution! (There are currently 7 to this problem, but that doesn't mean there can't be more.)
There is nothing stating that all steps taken are upward, so the answer is infinity, as someone can keep stepping backwards
It is the 11th term of fibonnaci but i would like to understand the reason better.
wolfram input: sum(C(n,2n-11)), n=6 to 11 // result = 144 // 2 2 2 2 2 1 // 2 2 2 2 1 1 1 // 2 2 2 1 1 1 1 1 // 2 2 1 1 1 1 1 1 1 // 2 1 1 1 1 1 1 1 1 1 // 1 1 1 1 1 1 1 1 1 1 1 // C(a,b) = Combinations = a! /(a-b)! b!
Relevant wiki: Fibonacci Sequence
The person can use 144 different ways to reach the top.
wolfram input: sum(C(n,2n-11)), n=6 to 11 // result = 144 // 2 2 2 2 2 1 // 2 2 2 2 1 1 1 // 2 2 2 1 1 1 1 1 // 2 2 1 1 1 1 1 1 1 // 2 1 1 1 1 1 1 1 1 1 // 1 1 1 1 1 1 1 1 1 1 1 // C(a,b) = Combinations = a! /(a-b)! b!
From the problem, we can get the equation x + 2 y = 1 1 such that x , y ∈ N Using some logical reasoning, we see that x is always odd while y can be even or odd. Using this information, we list out all possible coordinates: ( 1 1 , 0 ) , ( 9 , 1 ) , ( 7 , 2 ) , ( 5 , 3 ) , ( 3 , 4 ) , ( 1 , 5 ) For each coordinate, there is a number of combinations. ( 1 1 , 0 ) : ( 1 1 1 1 ) = 1 ( 9 , 1 ) : ( 1 9 + 1 ) = 1 0 ( 7 , 2 ) : ( 2 7 + 2 ) = 2 ! ⋅ 7 ! 9 ! = 3 6 ( 5 , 3 ) : ( 3 5 + 3 ) = 5 ! ⋅ 3 ! 8 ! = 5 6 ( 3 , 4 ) : ( 4 3 + 4 ) = 5 ! ⋅ 4 ! 7 ! = 3 5 ( 1 , 5 ) : ( 5 1 + 5 ) = ( 1 6 ) = 6 Adding all of these up, we get 1 + 1 0 + 3 6 + 5 6 + 3 5 + 6 = 1 4 4
In this case, I assume N = { 0 , 1 , 2 , … } , am I right?
A fairly simple way to view this problem would be to consider the fact that the man's trip to the top of the stairs is the result of moving up one or two stairs. In other words, the trip up the stairs can be expressed as a sum comprising of only 1's and 2's. For example, if we only wanted the man to go up the stairs one step at a time, our sum would be 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 . If we wanted the man to go 2 steps at a time until we got to step number 11, our sum would be 2 + 2 + 2 + 2 + 2 + 1 . Now, all we have to do is make a list of all of the unique sums we can make (each sum contains a different number of 1's and 2's). The possible sums are:
Sum 1: 2 + 2 + 2 + 2 + 2 + 1
Sum 2: 2 + 2 + 2 + 2 + 1 + 1 + 1
Sum 3: 2 + 2 + 2 + 1 + 1 + 1 + 1 + 1
Sum 4: 2 + 2 + 1 + 1 + 1 + 1 + 1 + 1 + 1
Sum 5: 2 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1
Sum 6: 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1
All we need to do is figure out how many equivalent expressions we can make out of our sums. To do this, we use the binomial coefficient for each of the expressions, considering the fact that the equivalent expressions are all created using the same numbers in different positions due to the Communitive Law of Addition. Sum 1 contains 6 numbers, and 5 of those numbers are 2's, so the binomial coefficient of Sum 1 would be ( 5 6 ) = 6. For each sum, you should get the following:
Sum 1: ( 5 6 ) = 6
Sum 2: ( 4 7 ) = 35
Sum 3: ( 3 8 ) = 56
Sum 4: ( 2 9 ) = 36
Sum 5: ( 1 1 0 ) = 10
Sum 6: ( 0 1 1 ) = 1
Add the six numbers together and you get 1 4 4 possible ways.
Nicely done! This is one way to avoid using recurrence relation.
I will use "hop" to refer to the motion of stepping and "stair" to refer to what the problem refers to as steps. The number of possibilities is equal to the number of sequences ( a 1 , … , a k ) where ∑ i = 1 k = 1 1 and a i ∈ { 1 , 2 } for all i . Note that the sequence is of length k if and only if there are exactly ( 1 1 − k ) hops of 2 stairs. Since the 1 -stair hops and 2 -stair hops can happen in any order, there are a total of ( 1 1 − k k ) ways to climb the stairs with exactly k hops. Clearly k can range from 6 to 1 1 , so the total number of ways this can be done is ∑ k = 6 1 1 ( 1 1 − k k ) = ( 5 6 ) + ( 4 7 ) + ( 3 8 ) + ( 2 9 ) + ( 1 1 0 ) + ( 0 1 1 ) = 6 + 3 5 + 5 6 + 3 6 + 1 0 + 1 = 1 4 4
Yes, you're essentially doing stars and bars .
Note that the final sum represents a "shallow sum" of a pascal triangle, can you compute that sum with minimal arithmetic?
else return Numero(n-1) + Numero(n-2);
Yeah, the most important part is explaining why this step is true. Can you explain why?
Sum of combinations of (6:5), (7:4), (8:3), (9:2), (10:1), (11:0) = 144
First number represents total steps, second number represents the number of double steps.
How about ( 5 : 6 ) , ( 4 : 7 ) , ( 3 : 8 ) , ( 2 : 9 ) , ( 1 : 1 0 ) , ( 0 : 1 1 ) , don't you have to consider them?
Note it down it will be better to solve
1 (2 steps) at a time and 9 (1 steps) at a time = 10! / 9!
2 (2 steps) at a time and 7 (1 steps) at a time = 9! / (7! x 2!)
3 (2 steps) at a time and 5 (1 steps) at a time = 8! / (5! x 3!)
4 (2 steps) at a time and 3 (1 steps) at a time = 7! / (4! x 3!)
5 (2 steps) at a time and 1 (1 steps) at a time = 6! / (5! x 1)
0 (2 steps at a time and 11 (1 steps) at a time = 11! / 11!
Total ways together = 10! / 9! + 9! / (7! x 2!) + 8! / (5! x 3!) + 7! / (4! x 3!) + 6! / (5! x 1) + 11! / 11!