Move a block on an incline by a minimum force

Relevant wiki: Solving for Equilibrium

Let us first draw the force diagram of the block.

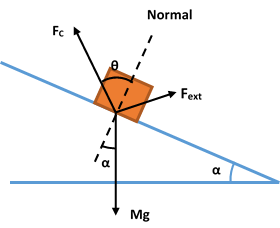
Three forces are acting on the block,
1) The gravitational force ( $Mg$ ): It is fixed in both the magnitude and the direction.
2) The contact force by the inclined plane ( $F_C$ ): It is the resultant of the friction and the normal reaction. In the static conditions, it makes a fixed angle $\theta$ with the normal such that $\tan \theta =\mu$ . However, its magnitude is not fixed and depends on the other forces acting on the body.
3) The external force ( $F_{\text{ext}}$ : It can be varied both in the direction as well as in magnitude.

For the object to remain in the equilibrium, the forces shown in the diagram should form a closed triangle on connecting them in order.

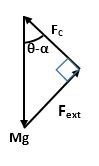
Now, the force $Mg$ and the direction of contact force is fixed. We can change the magnitude and the direction of the external force and simultaneously the magnitude of the normal will change to keep the triangle closed or the block stationary.

The shortest length of the external force vector would be the perpendicular length. Therefore, from the above diagram, we can conclude that ${F_{\text{ext}} = mg \sin(\theta -\alpha)}$

Putting the value $\theta = \arctan \mu$ , we get
$\boxed{F_{\text{ext}} = mg \sin(\arctan \mu -\alpha)}$ .