Think Geometry!
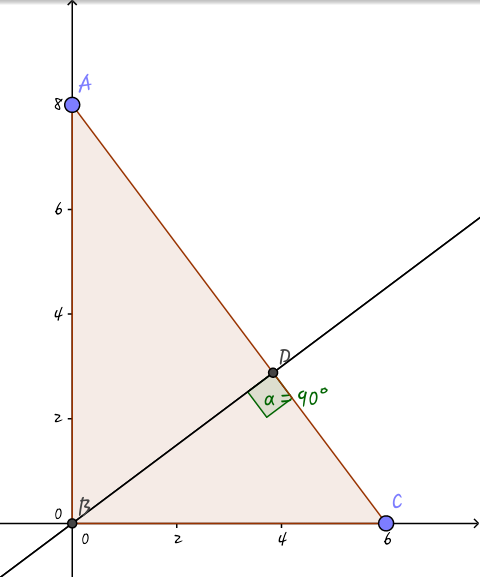
A right Δ A B C is drawn on the x − y plane as shown in the figure above.
If A B is 8 units and B C is 6 units, and the value of B D + C D is k , then enter the value of ⌊ 1 0 0 k ⌋ .
The answer is 840.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
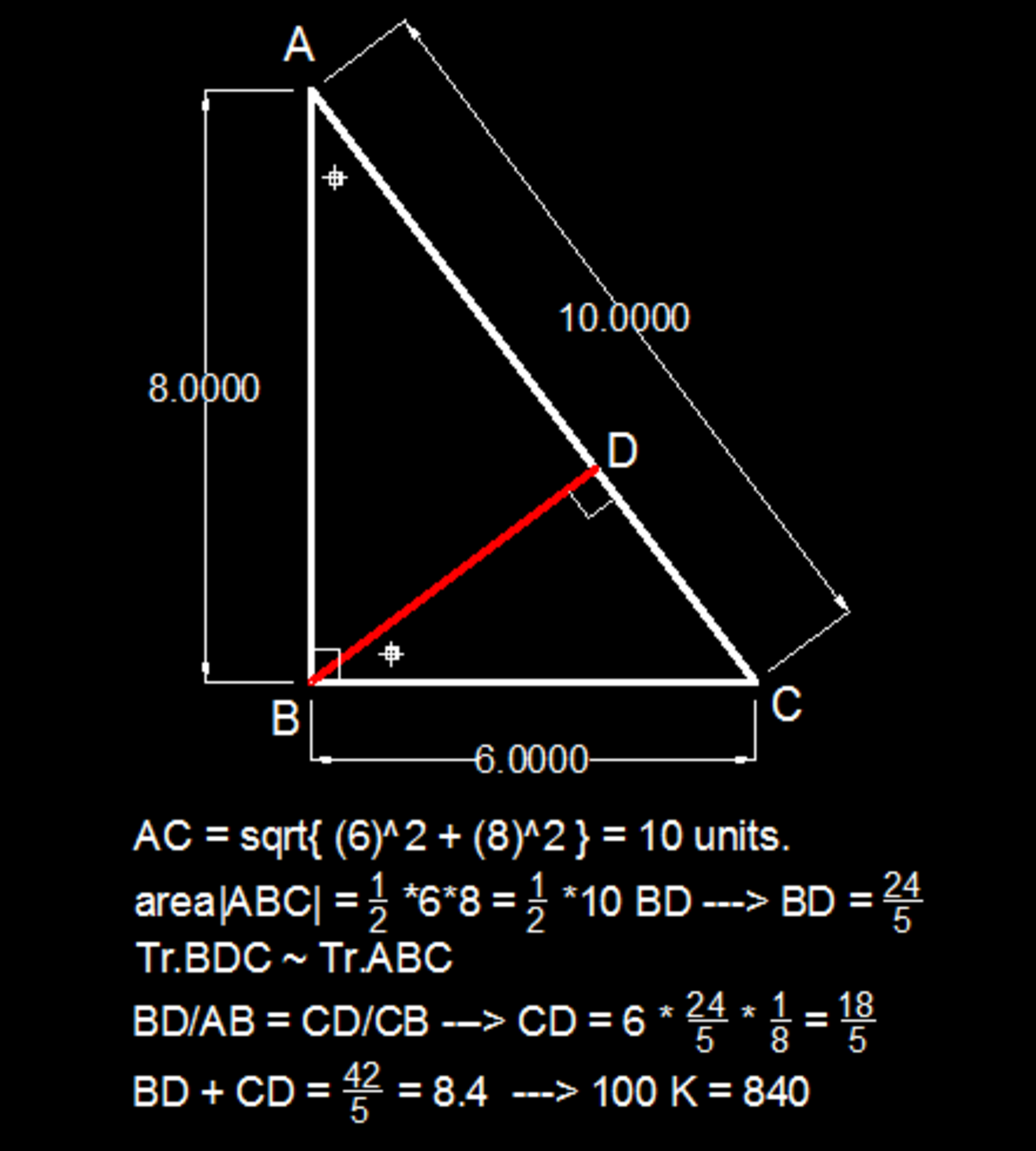
Nice solution (+1)!
Log in to reply
What seed level did you give it?
I don't think this should be a level 4 problem...
Lev4 :-) , its not that tough I know.
We note that △ B C D is similar to △ A B C . And △ A B C is a 3-4-5 Pythagorean triangle.
⟹ ⎩ ⎪ ⎨ ⎪ ⎧ B D = 5 4 B C C D = 5 3 B C ⟹ B D + C D = ( 5 4 + 5 3 ) B C = 5 7 × 6 = 8 . 4
⟹ ⌊ 1 0 0 k ⌋ = 8 4 0
That was quick and awesome solution sir! (+1)!
Elegant solution sir!
R i g h t Δ A B C i s 3 − 4 − 5 , ⟹ r i g h t Δ C D B i s a l s o 3 − 4 − 5 . B u t B C i s h y p o t e n u s e o f Δ C D B , D C t h e s m a l l s i d e . ∴ B C = 6 ∗ 5 5 , B D = 6 ∗ 5 4 D C = 6 ∗ 5 3 . ⟹ k = 6 ∗ 5 4 + 6 ∗ 5 3 = 6 ∗ 5 4 + 3 = 8 . 4 . ⌊ 1 0 0 k ⌋ = 8 4 0 .
B D = A C A B × B C
= 4 . 8 units.
B C ² = C D × A C
C D = 3 . 6 units
B C + C D = 8 . 4 = k units
⌊ 1 0 0 k ⌋ = 8 4 0 .