Think of a good Gaussian surface!

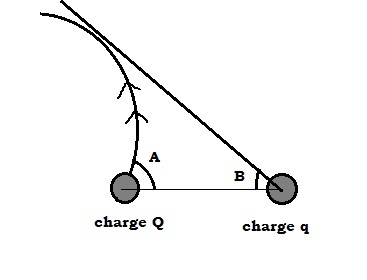
Two charges are placed along same horizontal line. Charge1 is carrying charge $Q$ . whereas charge 2 is carrying charge $q$ .If the field line emerging from charge 1 at an angle $A=30^\circ$ with horizontal goes to infinity and the tangent to that field line at infinity from charge 2 makes an angle $B=60^\circ$ with horizontal.

If $\dfrac Qq$ is of form $\dfrac{\sqrt a-b}{c}$ , where $a,b$ and $c$ are positive integers with $c$ minimized, find $a+b+c$ .