Think Ouside the Box
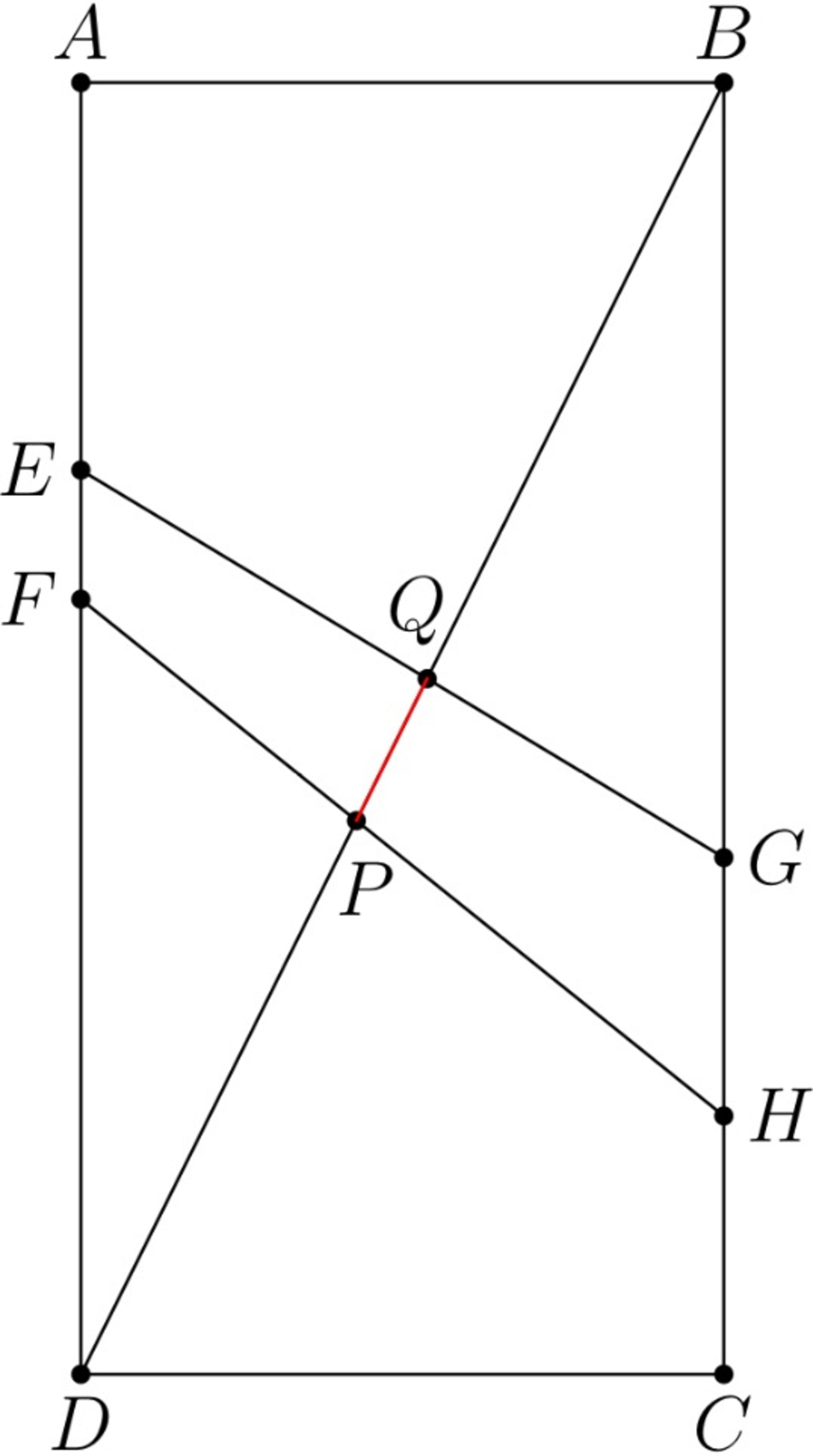
In rectangle A B C D , A B = 5 and B C = 1 0 . Points E , F , G , and H are on A D and B C in such a way that E F = 1 , G H = 2 , A E = 3 , and B G = 6 . E G and F H intersect diagonal B D at points Q and P , respectively. The length P Q can be expressed in the form z x y , where x , y and z are positive integers with y square-free and x , z coprime. Find x + y + z .
The answer is 146.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
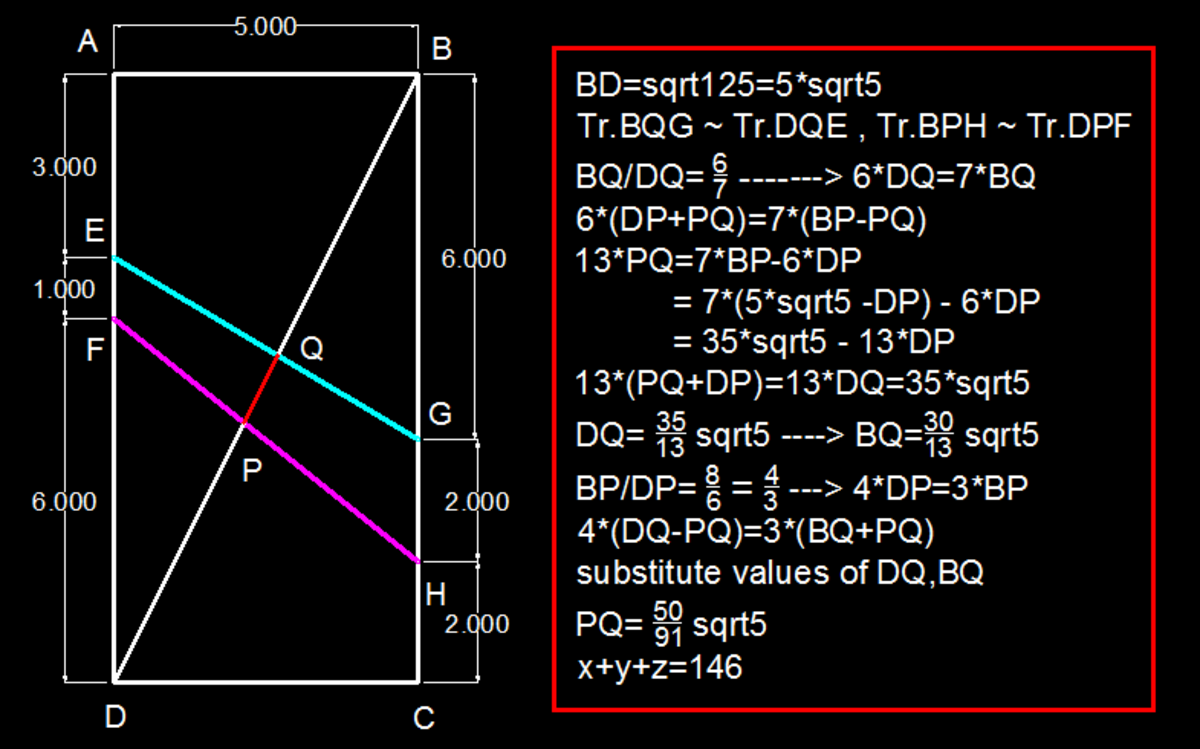
Missed, wrong calculation. However slightly different way.
Δ
B
A
D
,
H
y
p
o
t
e
n
u
s
e
B
D
=
5
2
+
1
0
2
=
5
5
.
Δ
B
Q
G
Δ
D
Q
E
∴
B
D
B
Q
=
B
G
+
D
E
B
G
=
1
3
6
Δ
B
P
H
Δ
D
P
F
∴
B
D
B
P
=
B
H
+
D
F
B
H
=
1
4
8
=
7
4
.
∴
Q
P
=
B
P
−
B
Q
=
{
7
4
−
1
3
6
}
∗
B
D
=
9
1
1
0
∗
5
5
=
9
1
5
0
5
=
z
x
y
.
x
+
y
+
z
=
1
4
6
.
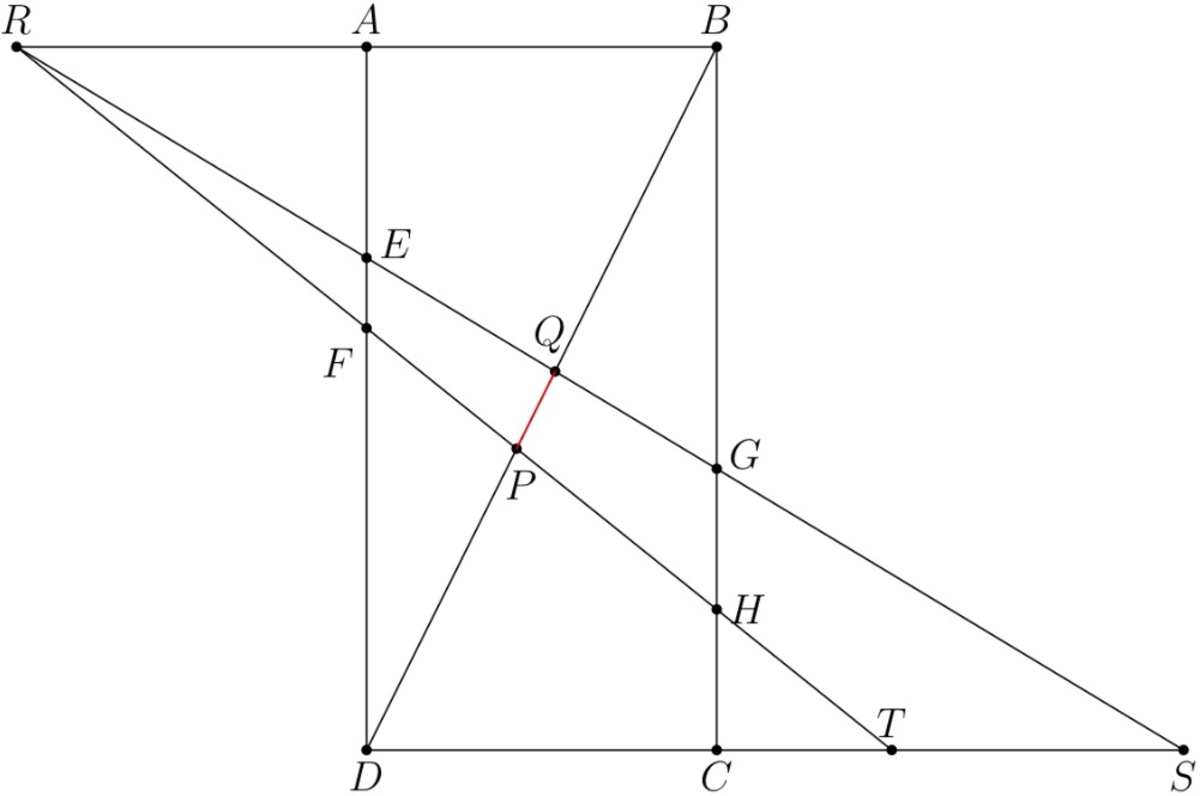
We can find the length of P Q by subtracting the length of D P from D Q .
We can extend E G , F H , and A B to meet at point R . We can also extend E G , F H , and D C to points T and S .
Since △ A E R and △ B G R are similar, this proportion becomes true:
A E A R = B G B R
Substituting in known lengths,
3 A R = 6 A R + 5
A R = 5
⟹ B R = 1 0
Since △ C G S and △ D E S are similar, this proportion becomes true:
C G C S = D E D S
Substituting in known lengths,
4 C S = 7 C S + 5
C S = 3 2 0
⟹ D S = 3 3 5
We also know that △ B Q R and △ D Q S are similar, where the ratio from △ B Q R to △ D Q S is 7 6 . So, B Q = 7 6 D Q since they are corresponding sides. Note that B D = 5 5 . So,
D Q + 7 6 D Q = 5 5
D Q = 1 3 3 5 5
Since △ T C H and △ T D F are similar, this proportion becomes true:
C H C T = D F D T
Substituting in known lengths,
2 C T = 6 C T + 5
C T = 2 5
⟹ D T = 2 1 5
We also know that △ B P R and △ D P T are similar, where the ratio from △ B P R to △ D P T is 3 4 . So, B P = 3 4 D P since they are corresponding sides. So,
D P + 3 4 D P = 5 5
D P = 7 1 5 5
The length P Q , which we are asked to find, is P Q = D Q − D P = 1 3 3 5 5 − 7 1 5 5 = 9 1 5 0 5 . Therefore, x + y + z = 5 0 + 5 + 9 1 = 1 4 6 .
Note: This can also be done nicely using coordinate geometry .