Think out of the circle (1)

Geometry Level 3

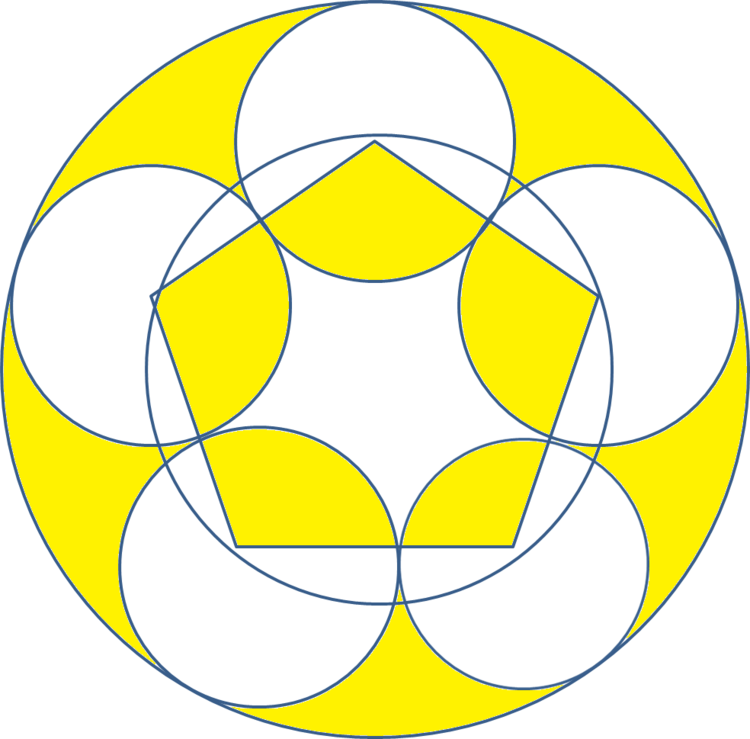Let $n$ be the diameter of the largest circle. If the radius of the smallest circle is 10, what can we confirm about $n$ ?

i) It is an irrational number;

ii) It is a prime;

iii) It is a whole number;

iv) It is lesser than 60;

v) The value is between 40 and 60.

Enter your answer by converting the Roman numerals into numbers, then multiply the correct answers.

The answer is 20.

1 solution

Marta Reece
Jan 27, 2017

The triangle connecting the center of the largest circle, the center of one of the smallest circles, and the point at which this small circle is tangent to another small circle is a right triangle with an angle at the center of the large circle being 36 $^\circ$ .The leg opposite that angle is 10, and hypotenuse is $\frac{n}{2}-10$ .

$sin(36^\circ)=$ $\frac{\sqrt{2(5-\sqrt{5})}}{4}$ $=\frac{20}{n-20}$

Solving for $n$ :

$n=20+\frac{40\times\sqrt{2}}{\sqrt{5-\sqrt{5}}}=54.026$

But frankly this problem is actually almost trivial. It is much too easy to guess that the answer is an irrational number not far short of 60.

Think out of the circle (1)

The answer is 20.

1 solution

0 pending reports