Is the answer still 2?
1 + x 2 x + 1 + x 4 x 2 + 1 + x x 3 + 1 + x 3 x 4
If x 5 = 1 with x = 1 , evaluate the value of the expression above.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Very nice different approaches!
I wonder if there is a way to interpret this expression more "holistically", esp since the substitution of x = 1 gives the correct numerical answer.
Ah nice approach! I was thinking of expressing the fraction as
x + 1 / x 1 + x 2 + 1 / x 2 1 + x 3 + 1 / x 3 1 + x 4 + 1 / x 4 1 ,
and each of x n + x n 1 can be expressed as an expression of x + x 1 = 2 − 5 ± 1 .
But your solution certainly easier!
Enough with the complex algebra. There is a fast way to solve this.
Multiplying 1 + x 2 x ⋅ x 3 x 3 + 1 + x 4 x 2 ⋅ x x + 1 + x x 3 + 1 + x 3 x 4
Which becomes x 3 + x 5 x 4 + x + x 5 x 3 + 1 + x x 3 + 1 + x 3 x 4 , but x 5 = 1 .
Hence 1 + x 3 x 4 + 1 + x x 3 + 1 + x x 3 + 1 + x 3 x 4 ⇒ 2 ⋅ ( 1 + x x 3 + 1 + x 3 x 4 ) .
Now you can try to sum the fractions, calculate the LCM, but this goes against my train of thought, which is multiply one of the fractions to be able to sum then up.
Multiply the first fraction 2 ⋅ ( 1 + x x 3 ⋅ x 2 − x + 1 x 2 − x + 1 + 1 + x 3 x 4 )
By the identity x 3 + 1 = ( x + 1 ) ( x 2 − x + 1 ) ,
2 ⋅ ( 1 + x 3 x 3 ⋅ x 2 − x + 1 + 1 + x 3 x 4 ) 2 ⋅ ( 1 + x 3 x 5 − x 4 + x 3 + 1 + x 3 x 4 ) 2 ⋅ ( 1 + x 3 x 5 − x 4 + x 3 + x 4 ) 2 ⋅ ( 1 + x 3 1 + x 3 ) 2 ⋅ ( 1 1 ) = 2
Now you guys could be wondering, how could I have this visualization? Algebraic intuition, and such. It will be polished only by training and time. Now some of my motivations to proceed this way: The apparent symmetry of the fractions, the order of powers of x and finally my approach, that you saw I didn't change, even after the first multiplications, i.e. if you start solving a problem by Approach A, you should keep this approach, which is more likely to solve the whole problem.
What is the difference between "calculate the LCM (I'm assuming LCM of the denominator)" and "multiply one of the fractions to be able to sum them up"? Aren't you doing that because L C M ( 1 + x 3 , 1 + x ) = 1 + x 3 ?
Log in to reply
I know this is very wrong, but I assumed that how isn't trivial that L C M ( 1 + x 3 , 1 + x ) = 1 + x 3 , someone would think that L C M ( 1 + x 3 , 1 + x ) = ( 1 + x 3 ) ( 1 + x )
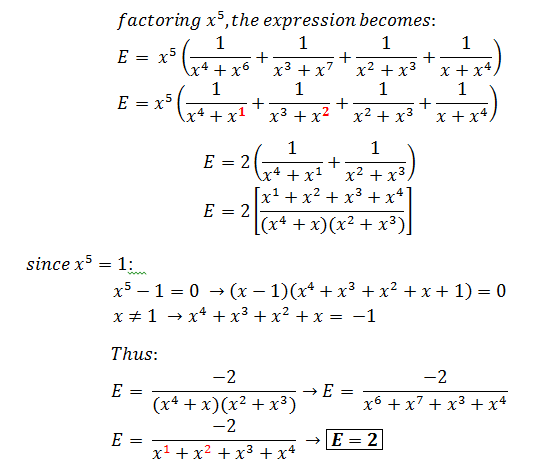
Method 1:
S = 1 + x 2 x + 1 + x 4 x 2 + 1 + x x 3 + 1 + x 3 x 4 = 1 + x 2 x + x ⋅ + x ⋅ x 4 x ⋅ x 2 + 1 + x x 3 + x 2 ⋅ + x 2 ⋅ x 3 x 2 ⋅ x 4 = 1 + x 2 x + 1 + x x 3 + 1 + x x 3 + 1 + x 2 x = 2 ( 1 + x 2 x + 1 + x x 3 ) = 2 ( ( 1 + x 2 ) ( 1 + x ) x + x 2 + x 3 + x 5 ) = 2 ( 1 + x + x 2 + x 3 1 + x + x 2 + x 3 ) = 2 Note that x 5 = 1
Method 2:
x 5 = 1 , x = 1 means that x is the fifth complex roots of unity or x = e 5 2 k π i , where k = 1 , 2 , 3 , 4 . Then,
S = 1 + x 2 x + 1 + x 4 x 2 + 1 + x x 3 + 1 + x 3 x 4 = 1 + x 2 x + 1 + x 4 x 2 + 1 + x 6 x 3 + 1 + x 8 x 4 = x + x − 1 1 + x 2 + x − 2 1 + x 3 + x − 3 1 + x 4 + x − 4 1 = e 5 2 π i + e − 5 2 π i 1 + e 5 4 π i + e − 5 4 π i 1 + e 5 6 π i + e − 5 6 π i 1 + e 5 8 π i + e − 5 8 π i 1 = 2 1 ( cos 5 2 π 1 + cos 5 4 π 1 + cos 5 6 π 1 + cos 5 8 π 1 ) = 2 1 ( cos 5 2 π 1 − cos 5 π 1 − cos 5 π 1 + cos 5 2 π 1 ) = cos 5 2 π 1 − cos 5 π 1 = cos 5 π cos 5 2 π cos 5 π − cos 5 2 π = cos 5 π cos 5 2 π − cos 5 4 π − cos 5 2 π = cos 5 π cos 5 2 π 2 1 = 2 sin 5 π cos 5 π cos 5 2 π sin 5 π = sin 5 2 π cos 5 2 π sin 5 π = sin 5 4 π 2 sin 5 π = sin 5 π 2 sin 5 π = 2 Note that x 5 = 1