Third Force
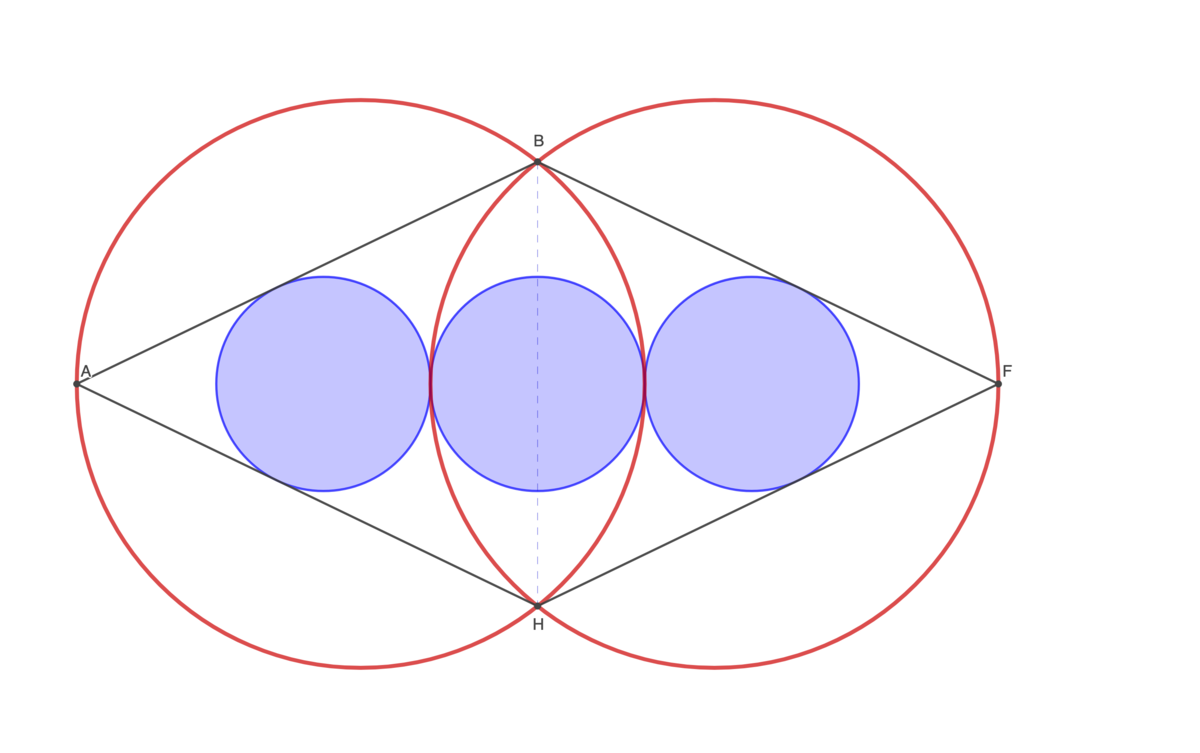
A B F H is a parallelogram with three congruent inscribed blue circles. The red circles are the circumcircles of △ A B H and △ B F H . They are also congruent. If the blue radius is 1, express the red radius as b − c a , where a and b are coprime and c is square-free. Submit a + b + c .
The answer is 29.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Label the diagram as follows:
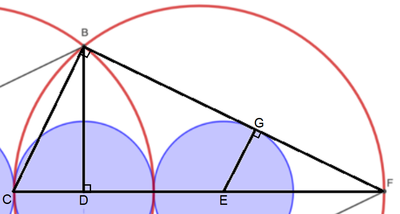
Let the red radius be r , so that C F = 2 r . Since the blue radius is 1 , C D = G E = 1 , D F = 2 r − 1 , and E F = 2 r − 3 .
By the Pythagorean Theorem on △ G E F , G F = ( 2 r − 3 ) 2 − 1 2 = 2 r 2 − 3 r + 2 .
By Thales's Theorem , ∠ C B F = 9 0 ° , so triangles △ B C F , △ G E F , △ C D B , and △ B D F are all similar to each other by AA similarity.
Since △ C D B ∼ △ B D F , B D C D = D F B D , or B D 1 = 2 r − 1 B D , which solves to B D = 2 r − 1 .
Since △ B D F ∼ △ G E F , B D D F = G E G F , or 2 r − 1 2 r − 1 = 1 2 r 2 − 3 r + 2 , which solves to r = 4 7 + 1 3 = 7 − 1 3 9 for r > 1 .
Therefore, a = 9 , b = 7 , c = 1 3 , and a + b + c = 2 9 .
Since the system is symmetrical about the y -axis, let us consider the right half. Let the radius the red circle be r and its center be C , the centers of the middle and the right blue circles be O and D r respectively, D E be perpendicular to B F , and ∠ O F B = θ . Then we have:
tan θ ⟹ sin θ = O F O B = O F B C 2 − O C 2 = 2 r − 1 r 2 − ( r − 1 ) 2 = 2 r − 1 2 r − 1 = 2 r − 1 1 = 2 r 1
We note that
sin θ 2 r 1 2 r 2 r 4 r 2 − 1 4 r + 9 ⟹ r = D F D E = 2 r − 3 1 = 2 r − 3 = 4 r 2 − 1 2 r + 9 = 0 = 4 7 + 1 3 = 7 − 1 3 9 Squaring both sides
Therefore a + b + c = 9 + 7 + 1 3 = 2 9 .