This could not be more imaginary
Let f ( n ) = a 1 n + a 2 n + a 3 n .
Given that
f ( 1 ) = a 1 + a 2 + a 3 = 0 f ( 2 ) = a 1 2 + a 2 2 + a 3 2 = i f ( 3 ) = a 1 3 + a 2 3 + a 3 3 = i i
and that − ( f ( 4 ) + f ( 7 ) ) = d a + b ( e c π )
Find a + b + c + d given that they are integers . . Assumptions
∙ i = − 1
∙ ( e ) is Euler's number or ( e = lim n → ∞ ( 1 + n 1 ) n )
. .
Try my Other Problems
The answer is 23.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Newton's sums are so tedious ;-;
Log in to reply
Till now I still have no idea how this is one of my most popular problems. Personally I hated it.
See my solution... although similar
I did same.
Yes, I used Newton's Sums method too. It is tedious but systematic. I am attempting to make it simpler here.
Let S 1 = a 1 + a 2 + a 3 S 2 = a 1 a 2 + a 2 a 3 + a 3 a 1 S 3 = a 1 a 2 a 3
Then by Newton's Sums we have:
⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ f ( 1 ) = S 1 = 0 f ( 2 ) = S 1 f ( 1 ) − 2 S 2 = 0 − 2 S 2 = i ⇒ S 2 = − 2 1 i f ( 3 ) = S 1 f ( 2 ) − S 2 f ( 1 ) + 3 S 3 = 0 − 0 + 3 S 3 = i i ⇒ S 3 = 3 1 i i f ( 4 ) = S 1 f ( 3 ) − S 2 f ( 2 ) + S 3 f ( 1 ) = 0 − ( − 2 i ) ( i ) + ( 3 i i ) ( 0 ) = − 2 1 f ( 5 ) = 2 i f ( 3 ) + 3 i i f ( 2 ) = 2 i i i + 3 i i i = 2 1 i i + 1 + 3 1 i i + 1 = 6 5 i i + 1 f ( 7 ) = 2 i f ( 5 ) + 3 i i f ( 4 ) = 2 i ( 6 5 i i + 1 ) + 3 i i ( − 2 1 ) = 1 2 1 ( 5 i i + 2 − 2 i i )
Therefore,
− ( f ( 4 ) + f ( 7 ) ) = 2 1 − 1 2 5 i i + 2 − 2 i i = 1 2 6 − ( − 5 i i − 2 i i )
= 1 2 6 + 7 i i = 1 2 6 + 7 ( e − 2 π )
⇒ a = 6 , b = 7 , c = − 2 and d = 1 2 ⇒ a + b + c + d = 2 3
Can someone explain to me how the Newton Sums work ? I don't really seem to get it. I do get that a1 + a2 + a3 its a root, but I can't seem to make a connection. Thanks in advance
Log in to reply
Radinoiu,
You may want to read this: http://www.artofproblemsolving.com/Wiki/index.php/Newton%27s_Sums
Also refer to Vieta's formulas. You can also practice Vieta's formulas on Brilliant.org. It should be in Algebra section.
For simplicity lets represent a 1 = x , a 2 = y & a 3 = z .
Hence x + y + z = 0 x 2 + y 2 + z 2 = i x 3 + y 3 + z 3 = 3 x y z = i i = e 2 − π
( x + y + z ) 2 = 0 ⟹ x 2 + y 2 + z 2 + 2 ( x y + y z + x z ) = 0 ∴ x y + y z + x z = 2 − i … … ( i )
Now ( x y + y z + x z ) 2 = 4 − 1 ⟹ x 2 y 2 + y 2 z 2 + z 2 x 2 + 2 x y z ( x + y + z ) = 4 − 1 ⟹ x 2 y 2 + y 2 z 2 + z 2 x 2 = 4 − 1 … … ( i i )
Now ( x 2 + y 2 + z 2 ) 2 = − 1 ⟹ x 4 + y 4 + z 4 + 2 ( x 2 y 2 + y 2 z 2 + z 2 x 2 ) = − 1 ⟹ x 4 + y 4 + z 4 + 2 × ( 4 − 1 ) = − 1 ∴ x 4 + y 4 + z 4 = f ( 4 ) = 2 − 1
Now ( x 3 + y 3 + z 3 ) ( x 4 + y 4 + z 4 ) = x 7 + y 7 + z 7 + x 3 y 3 ( x + y ) + y 3 z 3 ( y + z ) + x 3 z 3 ( x + z ) = x 7 + y 7 + z 7 − ( x 3 y 3 z + y 3 z 3 x + x 3 z 3 y ) = x 7 + y 7 + z 7 − x y z ( x 2 y 2 + y 2 z 2 + z 2 x 2 ) ⟹ 2 − 1 × e 2 − π = x 7 + y 7 + z 7 − e 2 − π × ( 4 − 1 ) ∴ x 7 + y 7 + z 7 = f ( 7 ) = 1 2 − 7 e 2 − π
So − ( f ( 4 ) + f ( 7 ) ) = 1 2 6 + 7 e 2 − π ∴ a = 6 , b = 7 , c = − 2 & d = 1 2
Hence correct answer is 2 3 .
Amazing!
Same thing but much less calculation than Newton's Sums
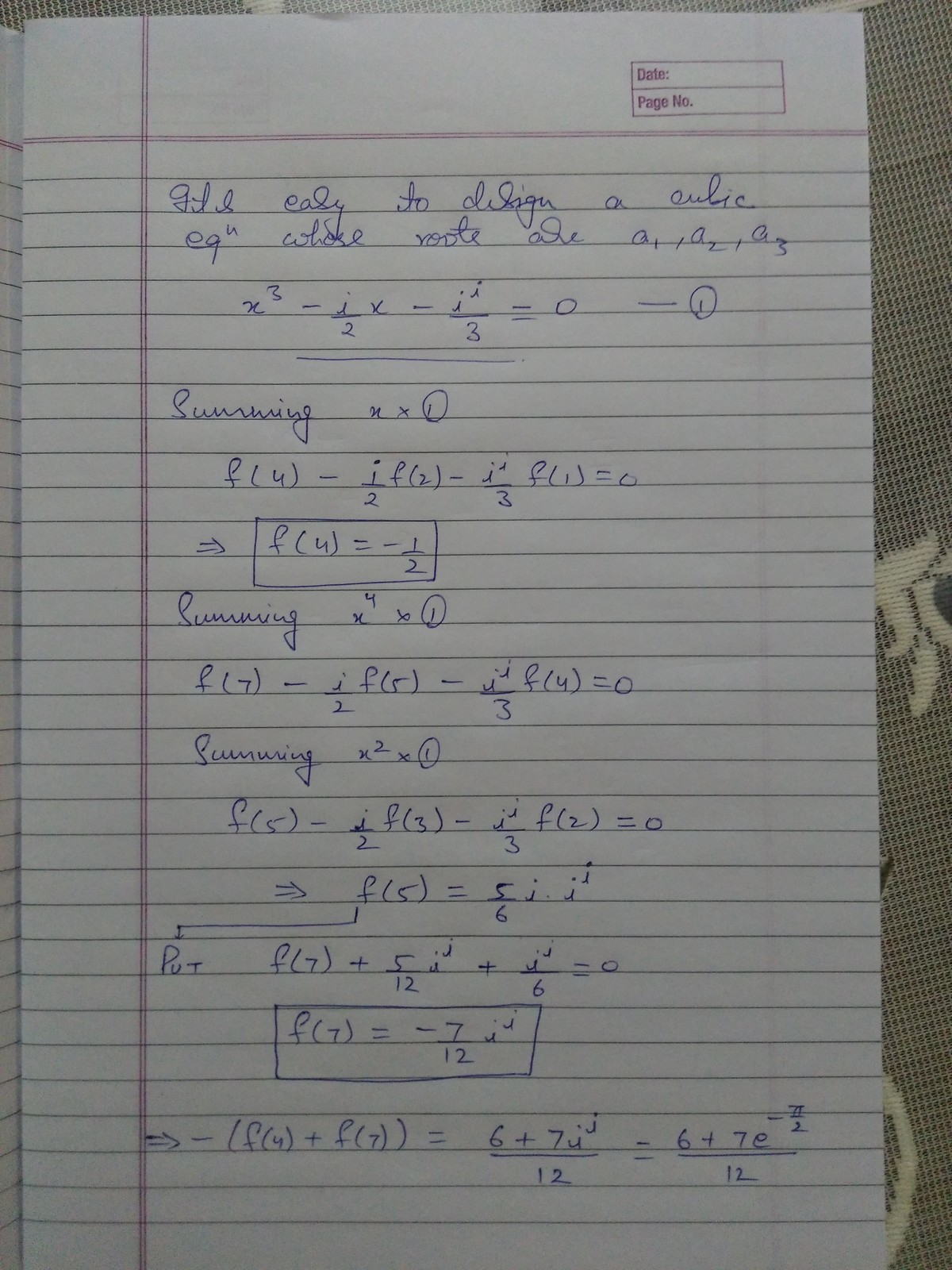
L e t z = i i ⇒ ln ( z ) = i ln ( i ) ⇒ ln ( z ) = i ln ( e i 2 π ) ⇒ ln ( z ) = − 2 π ⇒ z = e − 2 π
There is no statement that a,b,c,d are integers, nor positive.
Let S 1 = a 1 + a 2 + a 3 , S 2 = a 1 a 2 + a 1 a 3 + a 2 a 3 and S 3 = a 1 a 2 a 3 . Using Newton's sums we obtain:
f ( 1 ) = S 1
f ( 2 ) = S 1 2 − 2 S 2
f ( 3 ) = S 1 3 − 3 S 1 S 2 + 3 S 3
With the known values, the following system is formed;
S 1 = 0
S 1 2 − 2 S 2 = i
S 1 3 − 3 S 1 S 2 + 3 S 3 = i i
Solving that we get: S 1 = 0 , S 2 = − 2 i and S 3 = 3 i i .
By Newton's sums we know that f ( n ) = 2 i f ( n − 2 ) + 3 i i f ( n − 3 ) :
f ( 4 ) = 2 i f ( 2 ) + 3 i i f ( 1 ) = 2 i ( i ) + 3 i i ( 0 ) = − 2 1
f ( 5 ) = 2 i f ( 3 ) + 3 i i f ( 2 ) = 2 i ( i i ) + 3 i i ( i ) = 6 5 i ( i i )
f ( 6 ) = 2 i f ( 4 ) + 3 i i f ( 3 ) = 2 i ( − 2 1 ) + 3 i i ( i i ) = − 1 2 4 i i + 3 i
f ( 7 ) = 2 i f ( 5 ) + 3 i i f ( 4 ) = 2 i ( 6 5 i ( i i ) ) + 3 i i ( − 2 1 ) = − 1 2 7 i i
Hence, − ( f ( 4 ) + f ( 7 ) ) = 2 1 + 1 2 7 i i = 1 2 6 + 7 i i = 1 2 6 + 7 e − 2 π .
Comparing we get a = 6 , b = 7 , c = − 2 , d = 1 2 and a + b + c + d = 2 3 .