This familiar triangle again!
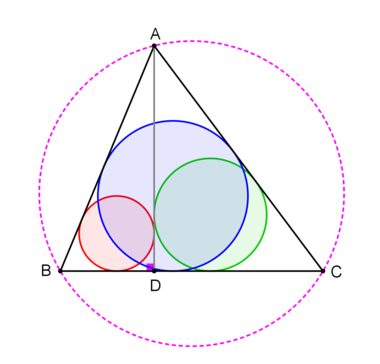
In , is one of its heights. The red, green and blue circles are the incircles of , and respectively. The radius of the blue circle is twice the radius of the red circle, while the radius of the green circle is . Moreover, the length of is three times the radius of the blue circle.
Find the circumradius of .
Side note: The idea came after dissecting, rearranging and stretching @Fletcher Mattox 's figure in Red, Blue and Greenish .
The answer is 8.125.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Typically, I am using the dirty Trigonometry to solve this pure and beautiful Geometry problem. Then again, I'm a Chinese. And whether it is a white cat or black cat, so long as it catches mice, it is a good cat. Specifically, I am using the fact that the line joining a vertex of a triangle to its incenter bisects the vertex angle.
Let the radius of the red circle be r , then the radius of the blue circle is 2 r and A D = 6 r . Let ∠ B A D = α . Consider the red circle and A D :
r cot 2 α + r cot 2 α + 1 ⟹ tan 2 α tan α = A D = 6 r = 6 = 5 1 = 1 − 2 5 1 2 ⋅ 5 1 = 1 2 5 ⟹ B D = 2 . 5 r , A B = 6 . 5 r
Similarly, for the green circle and A D :
3 cot 2 β + 3 tan 2 β = 6 r = 2 r − 1 1
The blue circle and A B :
2 r cot 2 α + β + 2 r cot 2 9 0 ∘ − α 4 ⋅ 5 1 + 2 r − 1 1 1 − 5 ( 2 r − 1 ) 1 + 4 ⋅ 1 − 5 1 1 + 5 1 r + 2 2 0 r − 1 2 + 6 2 0 r − 1 2 ⟹ r = 6 . 5 r = 1 3 = 1 3 = 7 r + 1 4 = 2 ⟹ tan 2 β = 3 1 , tan β = 4 3 , D C = 9
Then the circumradius R of △ A B C is given by:
2 R ⟹ R = sin ∠ B A C B C = sin ( α + β ) 5 + 9 = 5 6 1 4 ⋅ 6 5 = 8 6 5 = 8 . 1 2 5