Dielectrics

Electricity and Magnetism Level 3

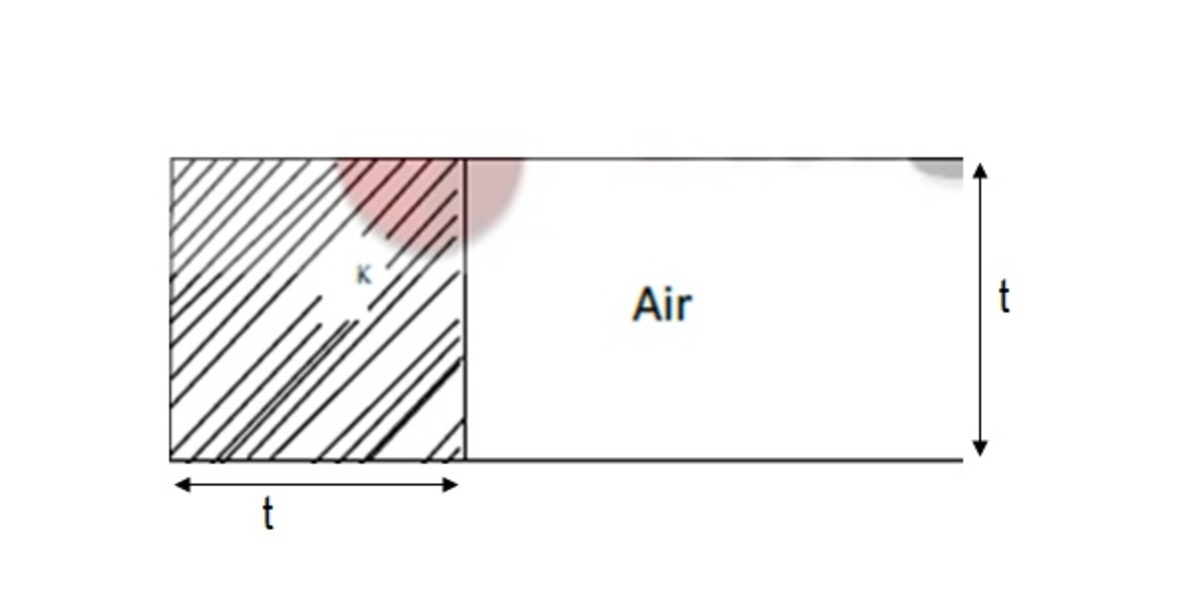
The capacitance of a parallel plate capacitor with air as dielectric is C. If a slab of dielectric constant $K$ and of the same thickness as the separation between the plates is introduced so as to fill 1/4th of the capacitor (shown in figure), then the new capacitance is

None

(K+2)\frac{C}{4}

(K+1)\frac{C}{4}

(K+3)\frac{C}{4}

K\frac{C}{4}

2 solutions

Nishant Rai
Apr 11, 2015

Let the capacitance of the lower part with dielectric be $C_1$ . Then $C_1 = \frac{KC}{4}$ where $C$ is the total capacitance of the conductor without Dielectric.

Capacitance $C_2$ of the upper part will be $\frac{3C}{4}$

Since both the capacitors are in parallel, $C_{net} = C_1 + C_2$

$C_{net} = \frac{(K + 3) C}{4}$ .

Kartik Sharma
Apr 28, 2015

We know that $C = \frac{K{\epsilon}_{0}A}{d}$ [Directly resulted from $P = \chi {\epsilon}_{0}E$

Now, previously $K = 1$ , so, $C = \frac{{\epsilon}_{0}A}{d}$

But then, 1/4th of the condenser is with K, so what's 1/4th? The area!

$C' = \frac{K{\epsilon}_{0}A}{4d}$

And, therefore, $C'' = \frac{3{\epsilon}_{0}A}{4d}$ , the remaining area.

${C}_{\text{new}} = C' + C'' = \frac{(K+3)C}{4}$

Dielectrics

2 solutions

0 pending reports