This is about squares
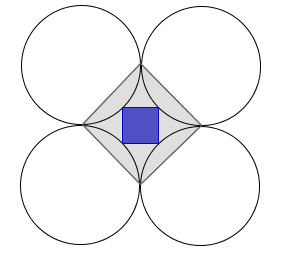With four tangent unit circles, we can form two squares. The large gray square is formed by the tangency points between the circles. The small blue one is formed by joining the midpoints of each arc that are formed by tangency points.
Find the difference of between the area of the gray square and that of the blue square to 2 decimal places.
The answer is 1.65685.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Well.. its exactly what I did..
That's how I solved it
I typed 1.6 and it said i'm wrong
Log in to reply
Said to two decimal places
it had to be 1.7 since you put only one number after the decimal point
I think I'm looking at this too simply. My solution rendered the wrong answer and it makes sense, but it doesn't. I just need some clarification. Figuring out the area of the grey square is easy. We know that the radius is 1, using Path theorum we know that the grey square's sides are √2, yielding an area (including the blue square) of 2. Figuring out the blue area seems easier to me than it really is. We know that the equilateral sides of your large triangle are 2, so the hypotenuse is 2√2. At this point, we subtract 2 from the hypotenuse to get the diagonal measurement of the blue square, yielding √2, which tells us that the sides of the blue square are 1 (which doesn't sound right). Why do we use the are of a rhombus formula instead of simply using the area of a square? Looking back at the figure, it seems impossible for the blue square to be just half the size of the grey square, so I must be wrong. I'm just looking for more of an explanation as to how and why.
Log in to reply
If the hypotenuse = 2√2, subtracting 2 does not yield √2, but rather 2√2 - 2. This is the path I took, but got a little confused from here trying to figure equilateral sides......anyone from here?
Log in to reply
Oh, duh. Yeah. That'd be my problem. 2√2 - 2 . I must be crazy.
You know that the diagonal of the blue square is 2 2 − 2
Let the side of the blue square be x
Then x 2 + x 2 = ( 2 2 − 2 ) 2
so 2 x 2 = ( 2 2 − 2 ) 2
But x 2 is the area of the blue square
Hence area of blue square is 2 1 ( 2 2 − 2 ) 2
Brilliant question. It took me a lot of time to solve it as I was not very sure how to find the area of blue square..
This is so simple, my solving contained finding the difference of the length of the parallels of a trapezoid(AE)/trapezium(BE), just to define the blue square's length, and now I feel kind of stupid but also proud, bc I got the answer right. :D
in any circle we can find a length of the big square as shown by Pythagoras theory that it will be
\sqrt { { 1 }^{ 2 }+{ 1 }^{ 2 } } =\sqrt { 2 } the area of it will be 2
and in the same circle the length between the center of the circle and the center of the blue square will be \sqrt { 2 } so that the half diameter of the square will be \sqrt { 2 } - 1 and the the diameter will be 2\sqrt { 2 } - 2 and the length of the blue square will be \frac { 2\sqrt { 2 } -2 }{ \sqrt { 2 } } \simeq \quad .586 and the area will be .343
so the difference is 2 - .343 = 1.656
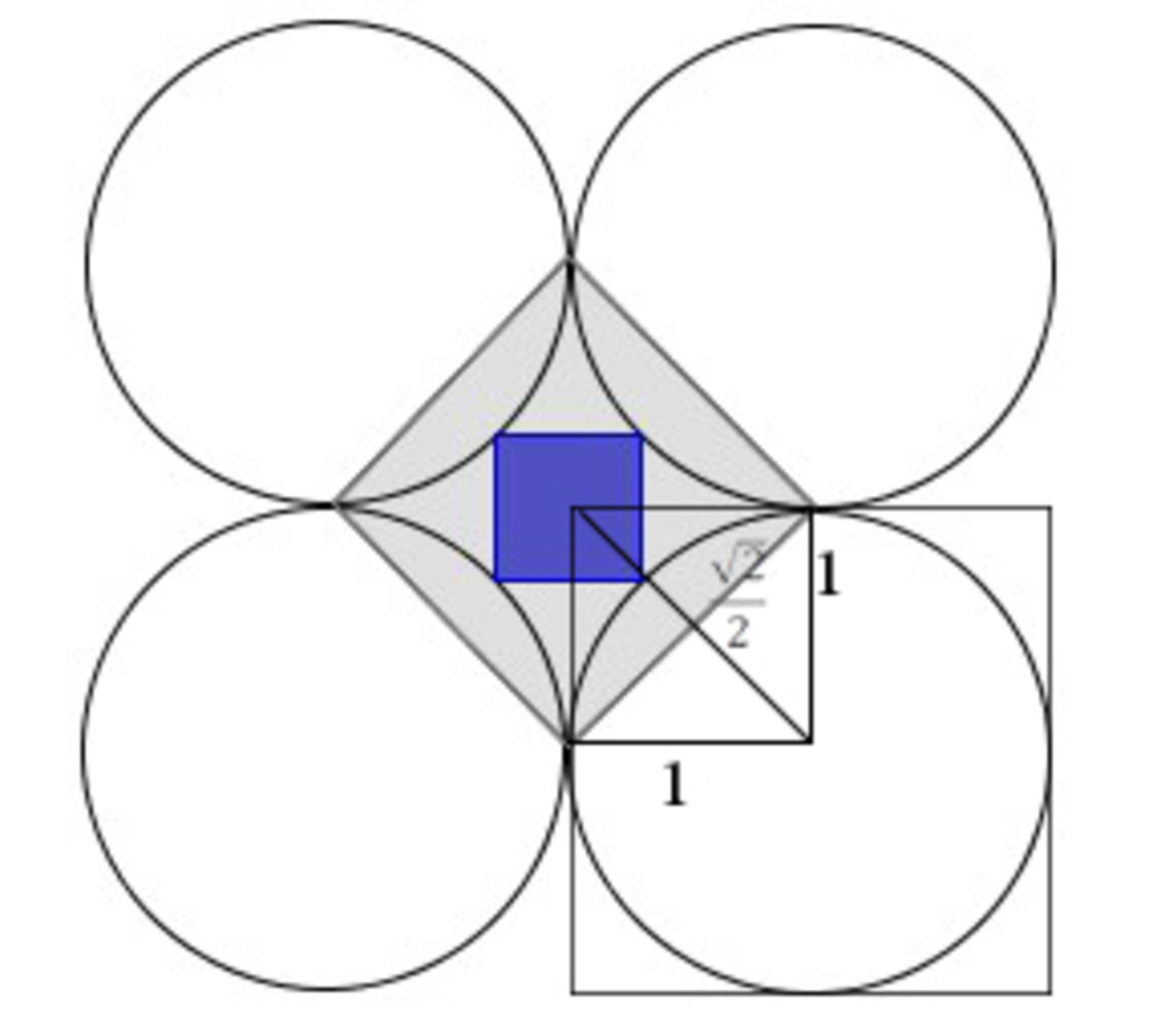
gray square area:
Its side is equal to 1 2 + 1 2 = 2 ∴ its area is 2
blue square area:
A diagonal of the square it is 2 2 − 2 . Then calculate its area as a robus' area ∴ its area is 2 ( 2 2 − 2 ) 2 = 6 − 4 2
The difference of areas is 2 − ( 6 − 4 2 ) = 4 2 − 4 ≈ 1 . 6 5 7