This is challenging...
 For
n
≥
3
, a pattern can be made by overlapping
n
circles, each of circumference 1 unit, so that each circle passes through a central point and the resulting pattern has order-
n
rotational symmetry.
For
n
≥
3
, a pattern can be made by overlapping
n
circles, each of circumference 1 unit, so that each circle passes through a central point and the resulting pattern has order-
n
rotational symmetry.
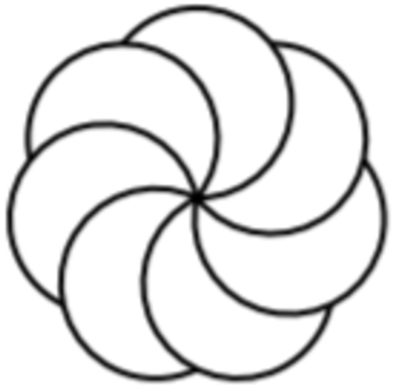
For instance, the diagram shows the pattern for n = 7 .
If the total length of visible arcs is 60 units, what is n ?
The answer is 118.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Some help please? https://brilliant.org/discussions/thread/i-dont-understand/
Each visible arc of a circle subtends an angle of π + n 2 π , so that the length of the arc is 2 1 + n 1 . The total length of the visible arcs is therefore 1 + 2 n , which measures 6 0 units. Therefore n = 1 1 8
 general formula
general formula
Circumference is given =1 (n+2)(pi)R=60
》{(n+2)2(pi)R}/2=60
》{(n+2)(1)}=120
》n=118👌
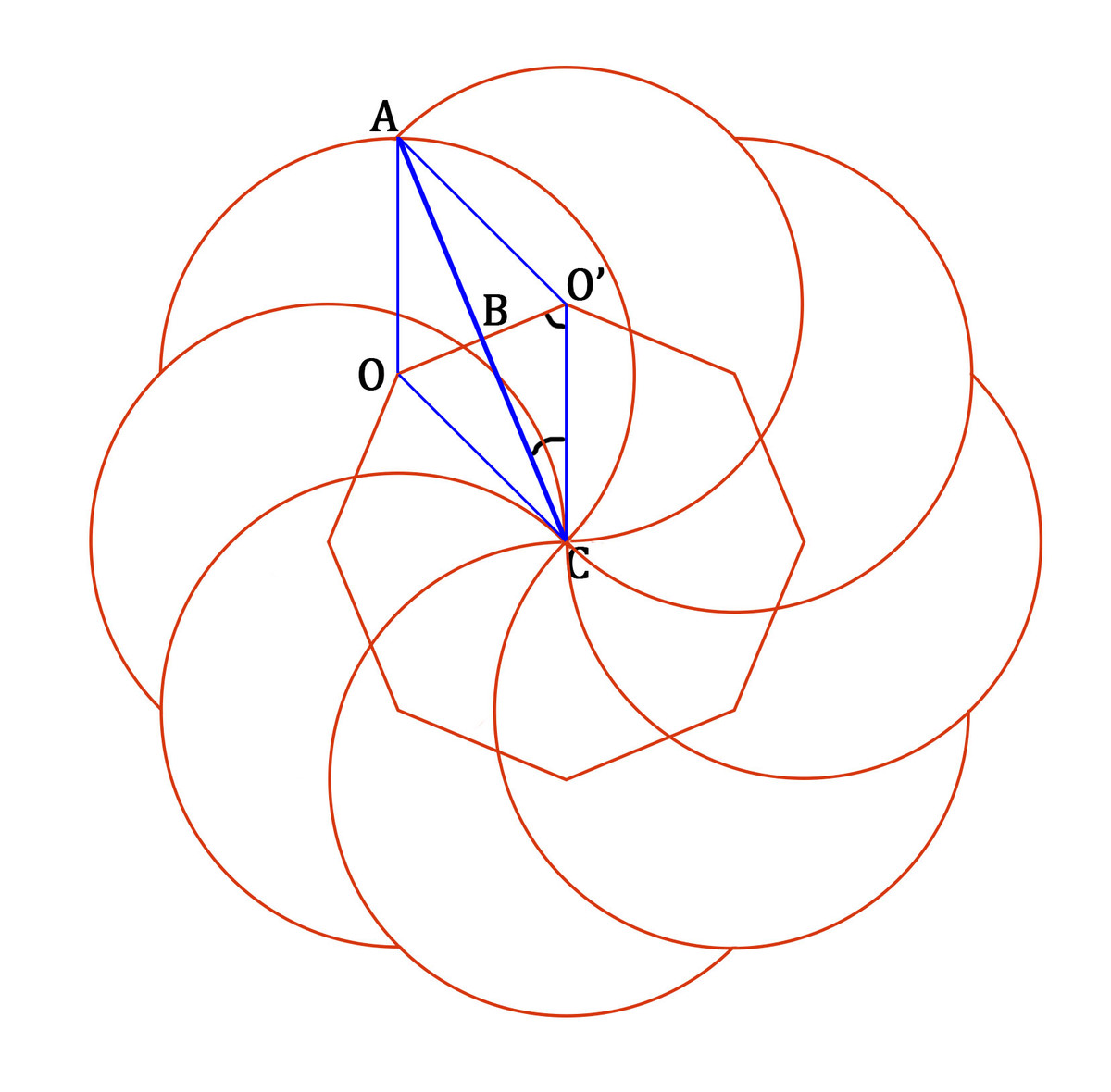 Joining the center of each adjacent circles we get a
n
-sided regular polygon whose circumcenter lies at point
C
, the common point of all the circles. Let the radius of each circle be
r
.
Joining the center of each adjacent circles we get a
n
-sided regular polygon whose circumcenter lies at point
C
, the common point of all the circles. Let the radius of each circle be
r
.
O C = O A = r = O ′ C = O ′ A ⇒ A O C O ′ is a rhombus. ⇒ A C ⊥ O O ′
∠ O C O ′ = n 2 π
⇒ ∠ B C O ′ = n π
⇒ ∠ B O ′ C = 2 π − n π = 2 n ( n − 2 ) π
⇒ ∠ A O ′ C = 2 ∠ B O ′ C = n ( n − 2 ) π
Length of visible arc of circle with center O ′ = Circumference of circle − invisible length of arc of circle with center O ′ = 1 − 2 π ∠ A O ′ C ⋅ circumference of circle = 1 − 2 n π ( n − 2 ) π ⋅ 1 = 2 n n + 2 … E q . 1
Length of visible arcs is 6 0 units.
Length of visible arc of circle with center O ′ = n 6 0 … E q . 2 Using E q . 1 and E q . 2 , we get n 6 0 = 2 n n + 2 ⇒ n + 2 = 6 0 × 2 = 1 2 0 ⇒ n = 1 1 8
For n overlapping circles, there are n points where the circumferences of adjacent circles meet which make up a regular n -side polygon. The two vertices of the polygon and the center point form an isosceles triangle inscribed in the circle. Let the arc extended by the side of the polygon to have a length of a and that by the equal side be b then the length of a visible arc of a circle is l = a + b . We note that a + 2 b = 1 , the circumference of a circle. Also that arc a extends an angle of n 4 π at the center of the circle. Then a = n 4 π × 2 π 1 = n 2 and b = 2 1 − a = 2 1 − n 1 , implying l = a + b = 2 1 + n 1 . Since there are n visible arcs in total, the total length of visible arcs is n l = 2 n + 1 . When 2 n + 1 = 6 0 , ⟹ n = 1 1 8 .