An algebra problem by I Gede Arya Raditya Parameswara

Algebra Level 5

Let $x,y,z$ be all real numbers such that $x+y+z=2$ .

What is the minimum value of $n = \sqrt{x^{2}+7}+\sqrt{y^{2}+11}+\sqrt{z^{2}+13}$ ?

Give your answer to 3 decimal places.

The answer is 9.774.

2 solutions

Mark Hennings
Feb 7, 2017

Appling the method of Lagrange multipliers, we need to solve the equations $\frac{x}{\sqrt{x^2+7}} \; = \; \frac{y}{\sqrt{y^2+11}} \; = \; \frac{z}{\sqrt{z^2+13}} \hspace{1cm} x + y + z = 2$ and these equations have the unique solution $x \; = \; \frac{2\sqrt{7}}{\sqrt{7}+\sqrt{11}+ \sqrt{13}} \hspace{1cm} y \; = \; \frac{2\sqrt{11}}{\sqrt{7}+\sqrt{11}+ \sqrt{13}} \hspace{1cm} z \; = \; \frac{2\sqrt{13}}{\sqrt{7}+\sqrt{11}+ \sqrt{13}}$ at which point $n \; = \; \sqrt{35 + 2\sqrt{77} + 2\sqrt{91} + 2\sqrt{143}} \; = \; \boxed{9.77472}$ Since $n$ is a positive function which diverges to infinity as any of $x,y,z$ tends to $\infty$ , it is clear that $n$ has no maximum value, but does have a minimum value. Moreover, the constraint domain $x+y+z = 2$ has no boundaries, and hence the minimum point will be identified by the method of Lagrange multipliers. Since the LM method produces just one extremum, it must be the desired minimum.

Good solution

I Gede Arya Raditya Parameswara - 4 years, 4 months ago

it is clear that $n$ has no maximum value, but does have a minimum value.

But why can't it be an inflection point? Is it because "you have shown that it has no maximum value, and the constraint domain has no boundaries, then it follows that whatever extremal value (single, not plural) that you've found must be a minimum value" ?

On the other hand, looking at the type of problems the author has posted, I'm pretty confident that this problem should be solved using some classical inequalities method. Maybe Cauchy-Schwarz inequality ? I'll be back on my drawing board...

Pi Han Goh - 4 years, 4 months ago

Since the function is positive, it must have an infimum. Since $n$ is a continuous function of $x,y,z$ which tends to infinity as $\Vert(x,y,z)\Vert \to \infty$ , we can restrict attention to a compact subdomain to see that the infimum must be a minimum. There is nothing stopping there being a saddle-point (the multi-dimensional version of an inflection), but the method of LM only finds one extremum. Since there is a minimum, that must be it, and there are no saddle-points.

Mark Hennings - 4 years, 4 months ago

I finally understood this statement. Thank you.

Pi Han Goh - 1 year, 4 months ago

Is there any way without using Lagrange's Multiplier ??

Kushal Bose - 4 years, 4 months ago

What is the shortest distance from $O$ to $C$ ? Obviously $\sqrt{(a+b+c)^2 + L^2}$ .

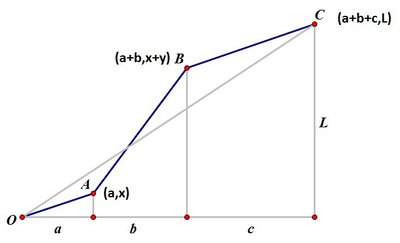
What is the distance from $O$ to $C$ if we go by straight line segments via $A$ and $B$ as shown (so that $O,A,B,C$ have fixed $x$ -coordinates and steadily increasing $y$ -coordinate)? Obviously $\sqrt{x^2 + a^2} + \sqrt{y^2 + b^2} + \sqrt{z^2 + c^2}$ where $x,y,z \ge 0$ and $x+y+z=L$ . Thus the minimum value of $\sqrt{x^2 + a^2} + \sqrt{y^2 + b^2} + \sqrt{z^2 + c^2}$ subject to the restrictions $x,y,z \ge 0 \hspace{1cm} x + y + z = L$ is $\sqrt{(a+b+c)^2 + L^2}$ if we choose $A,B$ to lie on the line segment $OC$ . Now put $a=\sqrt{7}$ , $b=\sqrt{11}$ , $c = \sqrt{13}$ , $L=2$ .

Mark Hennings - 4 years, 3 months ago

Wow ! Its excellent Sir .Thanks a lot

Kushal Bose - 4 years, 3 months ago

Clue: Pythagoras theorem

If you want a full solution, I don't mind doing it.

Julian Poon - 4 years, 3 months ago

Okk If you have time u can post it

Kushal Bose - 4 years, 3 months ago

Aakash Khandelwal
Apr 23, 2017

Let $\overline{ a} = x i + \sqrt {7}j$

$\overline{ b} = yi + \sqrt {11}j$

$\overline{ c} = z i + \sqrt {13}j$

Now we know

$| \overline {a } + \overline {b } + \overline {c} | \leq | \overline {a } | + |\overline {b } | + | \overline {c } |$

Thus answer follows.

An algebra problem by I Gede Arya Raditya Parameswara

The answer is 9.774.

2 solutions

0 pending reports