This is how I hula hoop
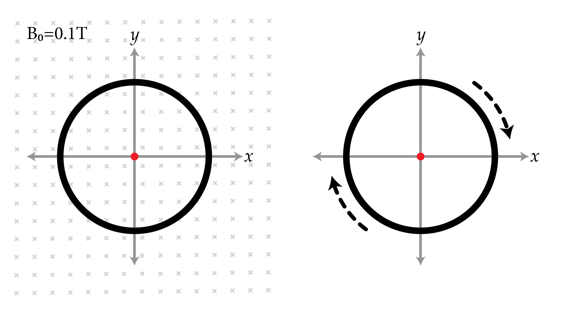
A uniformly charged nonconducting loop is placed so its center is at the origin. The normal to the loop is z ^ . There is also a homogeneous magnetic field of strength B 0 = 0 . 1 T in the - z ^ direction (i.e. perpendicular to the plane of the loop). This is shown in the figure on the left. Suddenly, the magnetic field is switched off and the loop begins to rotate about the z-axis as in the figure on the right. Determine the magnitude of the loop's final angular speed in rad/s if the specific charge to mass ratio of the loop is q / m = 1 0 − 1 C/kg .
The answer is 0.005.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
We know that the magnetic flux passing perpendicularly to any loop is given by ϕ = B A
Since the magnetic field is suddenly swicthed off there is change in magnetic flux passing through the loop and hence, an emf will be induced.
e = d t d ϕ and also e = 2 π r E Plugging the value of flux into above equation and equating we get
2 π r E = d t d B A ,
E = 2 d t r d B
Hence , force on loop is given by F = q E = 2 d t q r 2 d B
Net moment on the loop is
M = r F = I d t d ω
You get finally 2 d t q r 2 d B = d t m r 2 d ω
This implies d ω = 2 m q d B
Integrating both the sides you will get
ω = 0 . 0 0 5 r a d / s
ω = I L = I 1 ∫ d t M = = I 1 ∫ d t ∫ l o o p r d F = I r ∫ d t ∫ l o o p d q E = = I r d l d q ∫ d t ∫ l o o p d l E = I r d l d q ∫ d t ∫ a r e a d S d t d B = = I r d l d q ∫ a r e a d S ∫ d t d t d B = I r d l d q ∫ a r e a d S Δ B = = I r d l d q B 0 ∫ a r e a d S = m r 2 r 2 π r q B 0 π r 2 = = 2 1 m q B 0 = 2 1 × 1 0 − 1 C / k g × 0 . 1 T = 0 . 0 0 5 r a d / s
Very easy. d(flux)/dt= E(2πr) πr². d(B)/dt= E(2πr) Therefore Torque= Eqr=say, j jdt=qr(rdB/2) Integrating both sides L=Iw= mr²w=qr²(∆B/2) w=q∆B/2m w=5÷1000=0.005
First, we calculate the electric field inside the loop: 2 π r E = d t d Φ = π r 2 d t d B , so E = d t d B 2 r .
The moment of electric force is: M = E q r = d t d B 2 q r 2 .
We have: d L = M d t = d B 2 q r 2 or m r 2 d ω = d B 2 q r 2 .
Therefore, ω = 2 m q B 0 = 0 . 0 0 5 r a d / s .