This is Insanity !!!
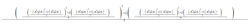 If the value of the gigantic term is
, where (
), then the value of
is?
If the value of the gigantic term is
, where (
), then the value of
is?
PS: Someone requested for clarification. I would like to say to them that the problem is totally legible. Open the image in a new window, then you would get what it is. Formatting it with LATEX would have been cumbersome. This is an original problem.
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let f ( x ) = 7 x 2 + 2 x , so the equation we want to solve is simply f ( f ( f ( f ( a ) ) ) ) = a ⟹ f ( a ) = a
7 a 2 + 2 a = a ⟹ a 2 + 2 a = 7 a ⟹ a 2 − 5 a = 0
It has two solutions, a = 0 or a = 5 , but a is natural, hence a = 5 .