Area of a Triangle Just From a Circle?
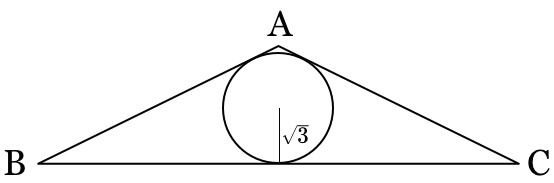
The given triangle is isosceles with vertex angle 1 2 0 ∘ and inradius of length 3 . In simplest form, the area of the triangle is a + b c . Find a + b + c .
The answer is 22.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
How did you get those angles ( 60 degrees and 15 degrees ) ?
Let O be the center of the incircle, D be the point of tangency of the incircle with side B C and E be the point of tangency of the incircle with side A B . Now as at most one interior angle of a triangle can be obtuse we know that ∠ B A C = 1 2 0 ∘ , and so ∠ A B C = ∠ A C B = 3 0 ∘ .
Next note that Δ O E A is similar to Δ B D A , and so ∠ A O E = ∠ A B D = 3 0 ∘ . Then with ∣ O E ∣ = ∣ O D ∣ = 3 we have that ∣ O A ∣ = ∣ O E ∣ sec ( 3 0 ∘ ) = 3 ∗ 3 2 = 2 .
Thus ∣ A D ∣ = ∣ A O ∣ + ∣ O D ∣ = 2 + 3 , and so ∣ B D ∣ = ∣ A D ∣ cot ( 3 0 ∘ ) = ( 2 + 3 ) ∗ 3 = 3 + 2 3 .
But the area of Δ A B C equals
2 1 ∣ A D ∣ ∗ ∣ B C ∣ = ∣ A D ∣ ∗ ∣ B D ∣ = ( 2 + 3 ) ( 3 + 2 3 ) = 6 + 4 3 + 3 3 + 6 = 1 2 + 7 3 .
Thus a + b + c = 1 2 + 7 + 3 = 2 2 .
L e t I D ⊥ B C = 3 . B D = D C , ∠ B = ∠ C = 3 0 o . ∴ T a n 2 1 B = 2 − 3 . = B D 3 ∴ B D = 2 − 3 3 = 3 ∗ ( 2 + 3 ) . A D = T a n B ∗ B D = 2 + 3 . ∴ A R E A o f Δ A B C = B D ∗ A D = 3 ∗ ( 2 + 3 ) 2 . Δ A B C = 1 2 + 7 3 = a + b c . ∴ a + b + c = 2 2 .
Yay, you didn't use trigonometry, just like me! Lol.
a=AC=AD+DC=ODcot(60)+ODcot(15) = 3 ( 3 1 ) + 3 ( 2 + 3 ) = 4 + 2 3 Now, ar(∆ABC)= 2 1 a 2 s i n ( 1 2 0 ) = 1 2 + 7 3 a=12, b=7, c=3 and a+ b+c=22