This is simple(but tricky!)
 Let
f
(
x
)
=
x
2
0
1
4
+
2
0
1
4
x
.
Let
f
(
x
)
=
x
2
0
1
4
+
2
0
1
4
x
.
Find ∫ 1 2 0 1 5 f − 1 ( x ) d x .
The answer is 1750.4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Awesome thinking....Mind blowing...
∫ a b f ( x ) d x + ∫ f ( a ) f ( b ) g ( x ) d x = b f ( b ) − a f ( a ) .Where g is the inverse function of f
We use substitution x = f ( u ) , d x = f ′ ( u ) d u
The limits of integration will be then:
For x = 1 , u 2 0 1 4 + 2 0 1 4 u = 1 = > u = 0 .
For x = 2 0 1 5 , u 2 0 1 4 + 2 0 1 4 u = 2 0 1 5 = > u = 1 .
By the definition of the inverse function, f − 1 ( f ( u ) ) = u .
Therefore,
∫ 1 2 0 1 5 f − 1 ( x ) d x = ∫ 0 1 u f ′ ( u ) d u
Integrating by parts:
∫ 0 1 u f ′ ( u ) d u = u f ( u ) ∣ 0 1 − ∫ 0 1 f ( u ) d u
= u ( u 2 0 1 4 + 2 0 1 4 u ) ∣ ∣ 0 1 − ∫ 0 1 u 2 0 1 4 + 2 0 1 4 u d u
= u ( u 2 0 1 4 + 2 0 1 4 u ) − 2 0 1 5 u 2 0 1 5 − ln 2 0 1 4 2 0 1 4 u ∣ ∣ ∣ ∣ 0 1
= 2 0 1 5 − 2 0 1 5 1 − ln 2 0 1 4 2 0 1 4 − ln 2 0 1 4 1 ≈ 1 7 5 0 . 4
Alright, now that's cool. But I have a few questions:
-
Your first substitution is due to the fact that f − 1 ( x ) = u , right?
-
Why did you bring g into this? I kinda get what you're trying to say, but I think it confuses a bit more.
-
How did you get u f ′ ( u ) in the integral?
-
Would there be a general solution for f ( x ) = x a + b x , ∫ c d f − 1 ( x ) d x ? If not, for f ( x ) = x a + a x ?
Thanks, Hassan.
Log in to reply
- Yes
- Sorry for that missing info in the solution, I am going to edit it :)
- I think This question now is answered, It was due to the mistake I've corrected it.(Just write the new integral in terms of variable u
- Alright I will think about the general solution, but I don't think it exist unless the limits of integration are 1 and a + 1 for f ( x ) = x a + a x
Good solution. This trick is much more obvious.
This one's the best solution. !
Consider a visual proof of integration by parts:
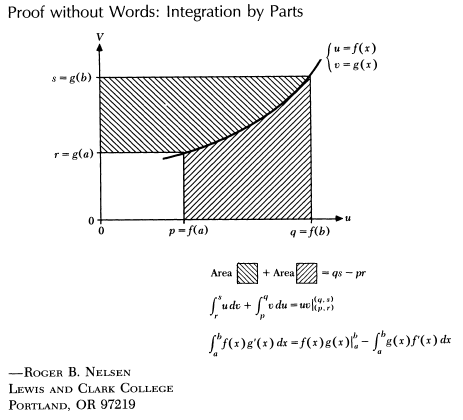
Note it's obvious that f ( 0 ) = 1 , f ( 1 ) = 2 0 1 5 and thus f − 1 ( 1 ) = 0 , f − 1 ( 2 0 1 5 ) = 1 . It follows by the above proof that f ( 1 ) ⋅ f − 1 ( 2 0 1 5 ) − f ( 0 ) ⋅ f − 1 ( 1 ) = ∫ 0 1 f ( x ) d x + ∫ f ( 0 ) f ( 1 ) f − 1 ( x ) d x
Simplifying, we find ∫ 1 2 0 1 5 f − 1 ( x ) d x = 1 ⋅ 2 0 1 5 − ∫ 0 1 ( x 2 0 1 4 + 2 0 1 4 x ) d x = 2 0 1 4 − [ 2 0 1 5 1 x 2 0 1 5 + lo g ( 2 0 1 4 ) 1 2 0 1 4 x ] 0 1 = 2 0 1 4 − 2 0 1 5 1 − lo g ( 2 0 1 4 ) 2 0 1 3 ≈ 1 7 5 0 . 4
substitute x=f(y) , , by inspection we get limits as 0 to 1 (corresponding to 1 and 2015)
Then you get integral of yf'(y) dy from 0 to 1, take y as first function and f'(y) as second and use IBP,, Fortunately the original function is very easy to integrate,, and ultimately u get 1750.40
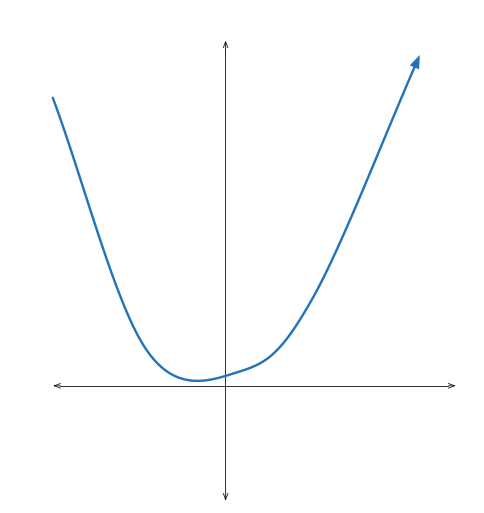
Taking the inverse of a function can be viewed as rotating the graph about the line y = x , i.e., interchanging the axes.
The graph of f ( x ) looks somewhat like this (on finding f ′ ( x ) , we see that it is positive for x ≥ 0 ). --
The area we need to find is that shaded, the area that f ( x ) makes with the y axis from y = 1 to y = 2 0 1 5 .
On some observation of f ( x ) , we see that it attains the value 2 0 1 5 at x = 1 .
So, the required area can be written as the area enclosed by f ( x ) with the x axis from 0 to 1 subtracted from a rectangle with length 2 0 1 5 units and breadth 1 unit.
Hence, ∫ 1 2 0 1 5 f − 1 ( x ) d x = 2 0 1 5 × 1 − ∫ 0 1 f ( x ) d x = 2 0 1 5 − ( 2 0 1 5 1 + lo g ( 2 0 1 4 ) 2 0 1 3 ) ≈ 1 7 5 0 . 4 1