A number theory problem
Pick 3 random points on the circumference of a circle and join them to form a triangle. What is the probability that the centre of the circle lies inside the triangle?
The answer is 0.25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The first point can go any where on the circle. But, when it is put, it makes the reference for the rest of the points. the second point would be randomly put and the probability density of it, with respect to the first point, is 2 π 1 . given the location of the first two points, the probability that the third point goes somewhere to make a desired triangle is 2 π θ . To see why, look at the pic below. the third point needs to be in the blue region, so we get a triangle, containing the centre point.
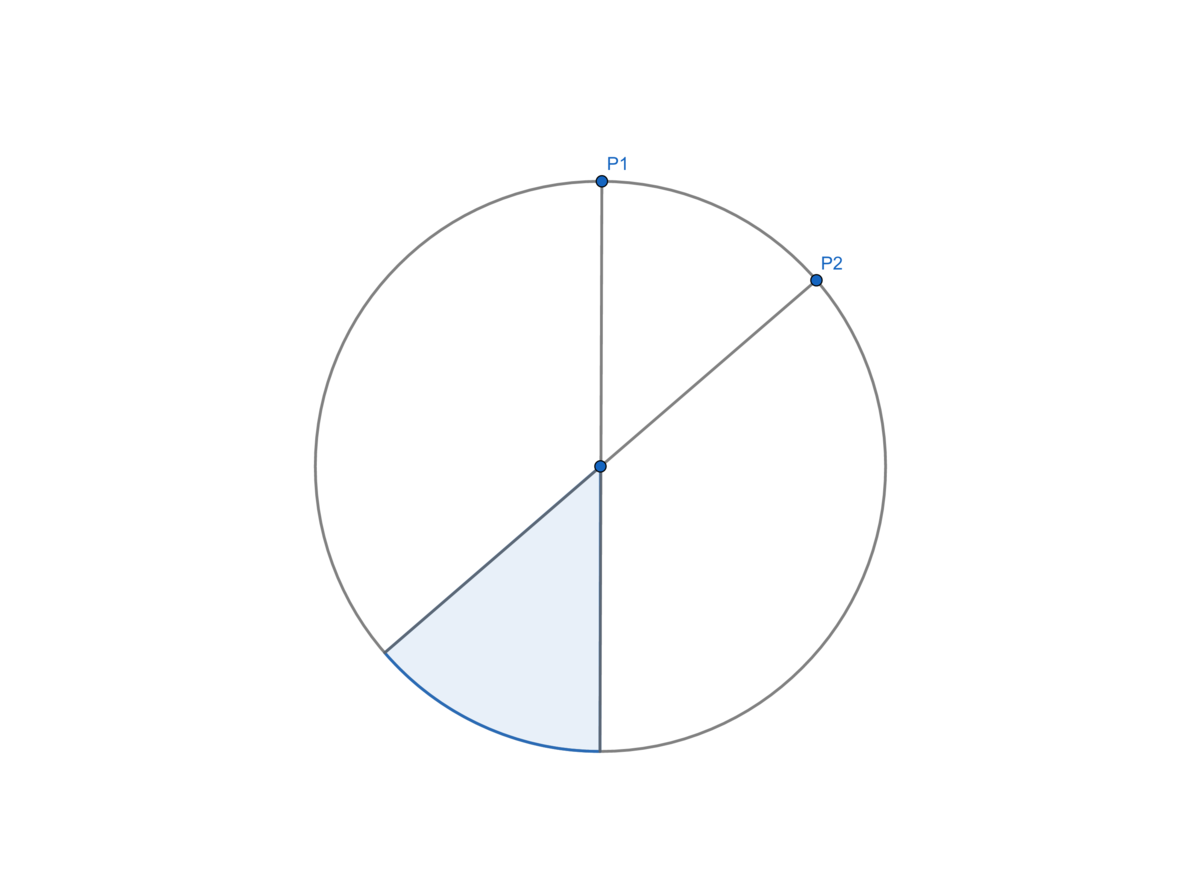
Then we may do integration.
2 × 2 π 1 ∫ 0 π 2 π θ d θ = 2 π 2 1 ( 2 θ 2 ) ∣ ∣ 0 π = 0 . 2 5
A very similar problem was already posted here. My solution is copied (with a slight modification) below.
Given two points A , B on a circle, the third point C must lie in the red region below if △ A B C is to contain the center: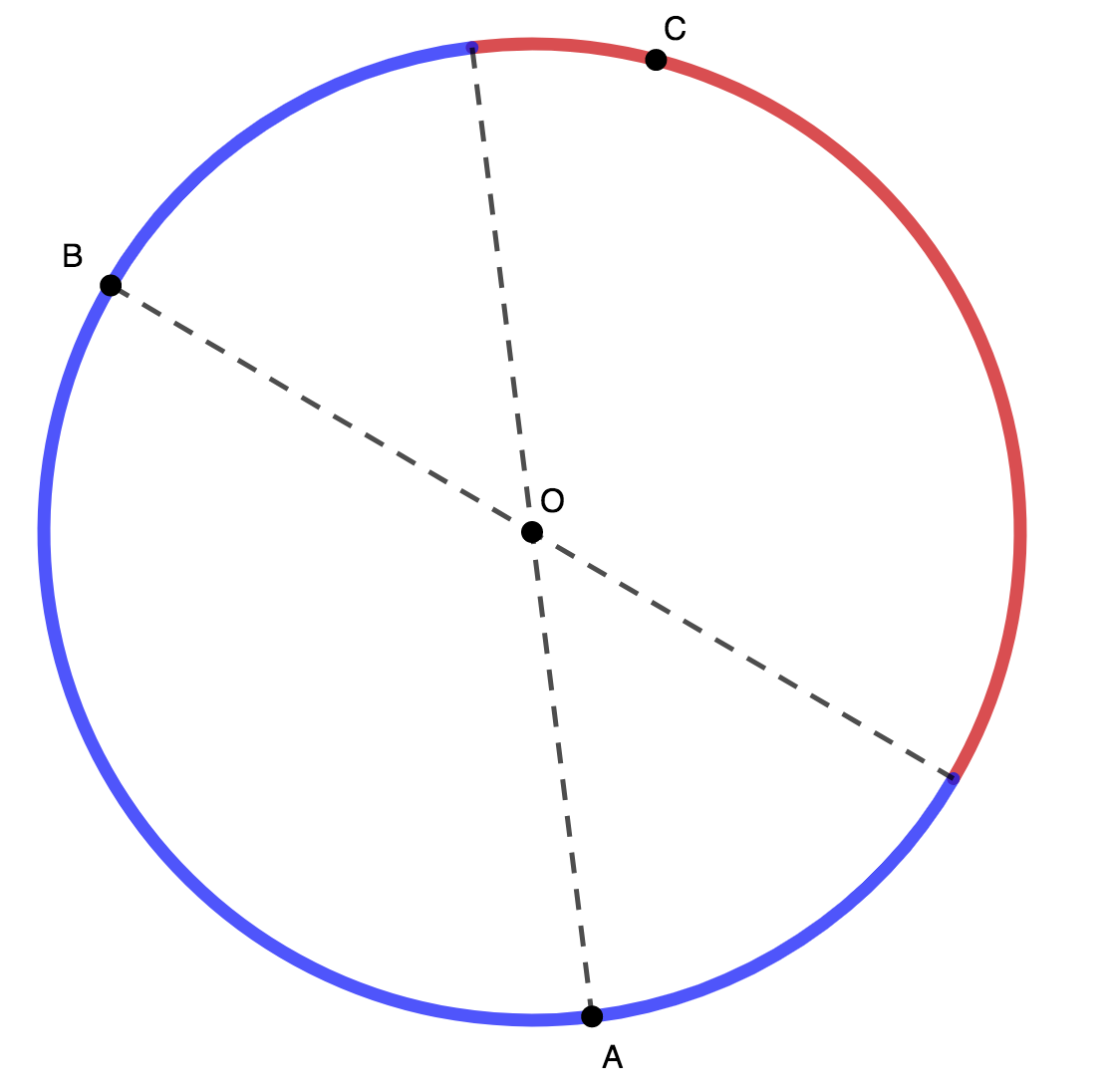
Now, we find the probability of this happening. Fix A and B on the circle, and let θ be the angle between them ( ∠ A O B ). Then 0 < θ ≤ π . Note that the angle intercepting the red region in the diagram is precisely θ . Thus the probability of a random point C being placed in the red area is 2 π θ . We integrate to compute the average probability over all possible θ : π − 0 1 ∫ 0 π 2 π θ d θ = π 1 [ 4 π θ 2 ] θ = 0 π = 4 π 2 π 2 = 4 1 = 0 . 2 5