This looks reasonable...(3)
A red square is formed when connecting the midpoints of the blue square. What if the blue shape were some other quadrilateral?
Connecting the midpoints of a quadrilateral's four sides forms a square.
Must the original quadrilateral be a square?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
Not all regular trapeziums work. For example, a rectangle is a regular trapezium, but we don't get a square.
Log in to reply
Thanks, I will change the solution. That rectangle should be a square.
This problem is ambiguous. Other quadrilaterals work, but only if four sides have equal lentghs. Rectangles work differently.
Log in to reply
What exactly is ambiguous? Also, not all the sides have to be equal, just look at the example Chew-Seong Cheong provided... (Kites can work too.)
Consider a square ABCD and anypoint P inside it and join P to all vertices. (The point P can be anywhere inside the square) Reflect point P about AB, BC, CD, DA. There will be a quadrilateral formed by there reflected points which need not be a square. [Consider drawing on paper and you'll understand]
This problem is a bit unclear. Is is asking for a non square quadrilateral that fulfills the requirement or a blanket statement that all quadrilaterals will work?
Log in to reply
How could you even consider it might be asking about all quadrilaterals?! There are obviously ones that don't work, so this wouldn't be much of a problem if that was the question...
Yes, I had the same idea when I read the quiz.
How do you show the angles in the red square are right angles?
Log in to reply
We started off with having a square inside and find to see if we can have a quadrilateral other than a square that can circumscribe the square with points of contact being the mid-points of sides and not the other way around. I, in fact, physically drew the figure to scale. The coordinates of the vertices of the red squares are ( 0 , 2 ) , ( 2 , 0 ) , ( 0 , − 2 ) , and ( − 2 , 0 ) . Those of the trapezium are ( 1 , 2 ) , ( 3 , − 2 ) , ( − 3 , − 2 ) , and ( − 1 , 2 ) .
The diagram representing the problem showed right angles on each corner, so nonsquare trapazoids were not possible.
Log in to reply
The issue is that such a diagram was merely representing the problem. Should the solution require that only a square with sides of about 1100 pixels be accepted? -.-
Also, by your reasoning, the problem's question can be trivially answered from the diagram. That's not much of a problem, then, is it? ;-)
can you help i don't understand what you said
Log in to reply
We are asked to see are there quadrilaterals (in blue) other than a square wholes mid-points are vertices of a square (red). I just showed that a regular trapezium is such a quadrilateral. Just shrink the top side of the original blue square equally left and right and stretch its bottom side equally left and right and we have the answer.
I don't either.
The quadrilateral can have a variety of shapes - the property that matters is: the diagonals are perpendicular and equal in length. All squares have this property but so do some kites and isosceles trapezoids. There are also irregular quadrilaterals with this property. So the answer is no .
I made an animation . Expanding a or b will allow for non-convex quadrilaterals although the outer quadrilateral loses some sides as the inequalities defining the sides become backward.
Great explanation! A figure would have been a nice addition. Good job!
Log in to reply
I did even better. Follow the link to an animation.
Cool animation!
excellent animation. thanks
Beautiful! But I must be missing something. Take an elongated rectangle - the result is a rhombus, not a square one.
Log in to reply
The animation only shows quads that lead to a square. You can't make an elongated rectangle.
Fantastic animation. Very very helpful to visualise the concept!
Excellent animation. But it is not ONLY Fantastic and Beautiful. It also gives a clue.
The out side quadrilateral must have the following properties.
(
1
)
I
t
s
h
o
u
l
d
h
a
v
e
e
q
u
a
l
d
i
a
g
o
n
a
l
s
.
T
h
i
s
m
a
k
e
s
t
h
e
i
n
s
i
d
e
f
i
g
.
w
i
t
h
e
q
u
a
l
a
l
l
s
i
d
e
s
.
(
2
)
T
h
e
d
i
a
g
o
n
a
l
m
u
s
t
b
e
a
t
r
i
g
h
t
a
n
g
l
e
s
.
T
h
i
s
m
a
k
e
s
t
h
e
i
n
s
i
d
e
f
i
g
.
w
i
t
h
a
l
l
a
n
g
l
e
s
a
s
r
i
g
h
t
a
n
g
l
e
s
.
T
h
e
r
e
s
u
l
t
:
O
u
t
e
r
q
u
a
d
r
i
l
a
t
e
r
a
l
c
a
n
N
O
T
b
e
:
−
a
r
e
c
t
a
n
g
l
e
,
a
k
i
t
e
o
r
a
∣
∣
g
r
a
m
,
(
a
l
l
t
h
r
e
e
)
,
w
i
t
h
a
l
l
s
i
d
e
s
e
q
u
a
l
.
a
n
i
s
o
s
c
e
l
e
s
t
r
a
p
e
z
i
u
m
w
i
t
h
d
i
a
g
o
n
a
l
s
N
O
T
a
t
r
i
g
h
t
a
n
g
l
e
s
,
a
r
h
o
m
b
u
s
w
i
t
h
u
n
e
q
u
a
l
d
i
a
g
o
n
a
l
s
.
N
o
s
y
m
m
e
t
r
y
i
s
a
n
e
c
e
s
s
i
t
y
.
There are many other shapes, not just a square. A rectangle for example would work as well. (If not, it worked in my mind)
The a rectangle does not work; it creates a parallelogram.
Here's a tip that always helps me and will probably help you: draw a picture. It's okay, though; math takes practice!
Rectangles, Rhomii, Parallelograms and Kites will not work. If I'd does then the mid points won't be connected
Log in to reply
Actually, if you see @Jeremy Galvagni 's solution, kites do work.
Also, you misspelled rhombi.
A rectangle is not valid.
at least he admitted he could be wrong, that is good.
Invalid invalid
Not a rectangle
I solved it pretty much the same way as everyone else, so I rather not repeat what has already been said.
But for completeness, here's counterexamples using dart and butterfly quadrilaterals.
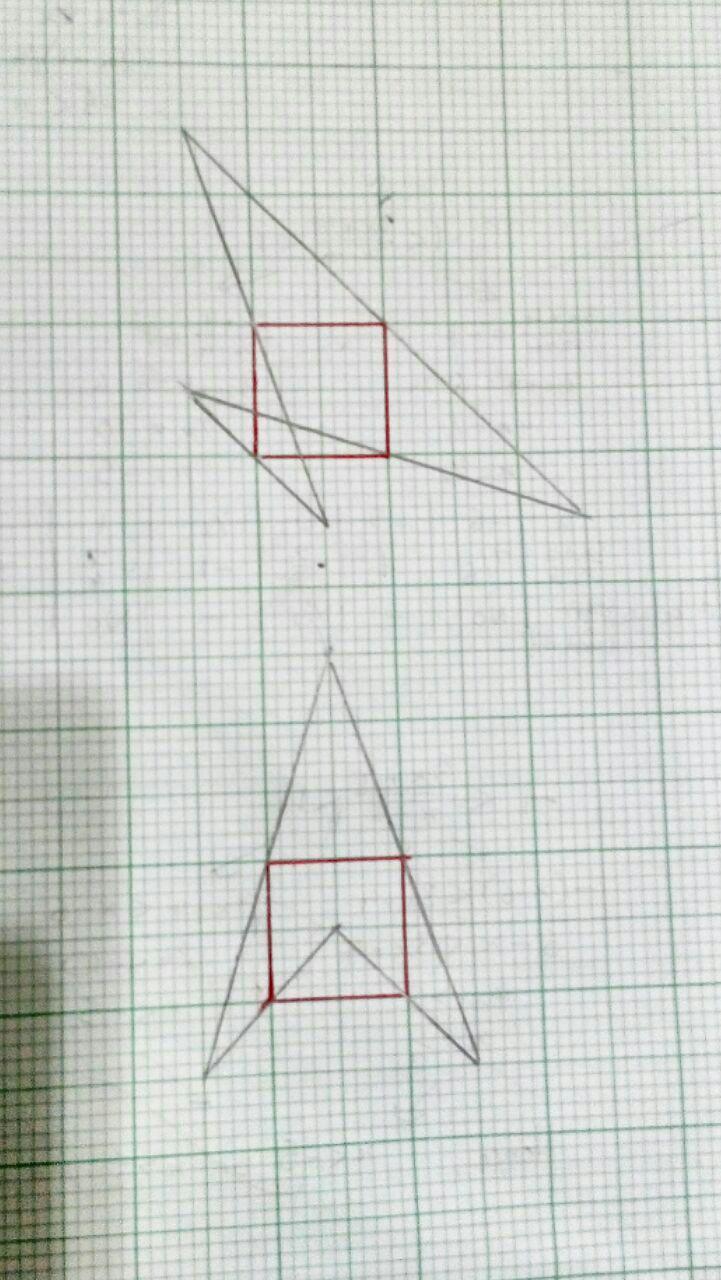
However I noticed that the surrounding blue quadrilateral has to share a line of symmetry with the red square, and maybe that's key to why some quadrilaterals (e.g. trapezoid, irregular) can't work.
By starting with two perpendicular diagonals of equal length and building the quadrilateral from that I found irregular quadrilaterals (no symmetry) which produced a square.
It doesn't have to have a line of symmetry at all. You can generate an entire continuum of quadrilaterals that have that red square as its midpoint polygon. See my solution. In the general case, the figure will be asymmetrical.
Self-crossing polygons don't count.
Given any quadrilateral, you can construct an infinite family of quadrilaterals of which the midpoints of the sides are the same as those of the original. Let A , B , C and D be the position vectors of the vertices of the original quadrilateral. Then the midpoints of the sides are 2 A + B , 2 B + C , 2 C + D and 2 D + A .
Let S be an arbitrary vector in the same plane. Then it's easy to see that the quadrilateral whose vertices have position vectors A + S , B − S , C + S and D − S will have the same midpoints of sides, and therefore the same quadrilateral will be formed by joining said midpoints.
If the original quadrilateral is a square, so that the midpoint quadrilateral is a square, then some of the quadrilaterals in the family will be kites, some will be isosceles trapezia, and some will be irregular.
Please can you explain your solution in simpler terms
Log in to reply
Start with the blue square in the original figure. The red square is its midpoint polygon. Then displace a pair of opposite vertices by the same vector, and displace the other pair of opposite vertices by the negative of this vector. The same red square will be the midpoint polygon of this new quadrilateral.
A kite is a counterexample.
If I join the midpoints of any quadrilateral I always get a Rhombus. Bt if the inner quadrilateral is a square the out must be a square too.
Log in to reply
You will always get a parallelogram. You are only guaranteed to get a rhombus if the outer quad has equal length diagonals.
Not all kites are counterexamples. You are guaranteed a rectangle, not always a square. If the kite as equal length diagonals, then you get a square.
If a square has 4 90 degree angles, then a rectangle with two opposing sides longer than the other two sides will create a quadrilateral, but not a square.
By playing around with a rough diagram of an irregular quadrilateral with midpoints connected to form a square I realised that 'removing' the central square produced 4 triangles. Two opposite triangles could be joined together (just by translation not by rotation) to form a half-size version of the original quadrilateral (with one diagonal, formed by the join of the two triangles). This could be done in one of two ways. The resulting half-size quadrilateral had the property that its diagonals were of equal length and met at a right angle.
I then, with more care (actually using a ruler this time) constructed a small quadrilateral by starting with two perpendicular diagonals of equal length. Then 'expanded' it by doubling the length of each side whilst keeping the same orientation. And hey presto, I came up with a diagram which, to my naked eye at least, was an irregular quadrilateral with the connected midpoints forming a square.
No , it needs not to be a square. A regular trapezium circumscribing the internal quadrilateral is a counter example.