This man is crazy
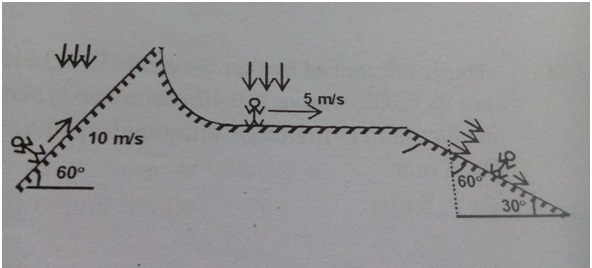 Figure above depicts a situation when it's raining (as shown by arrows) and the man is moving on the track. Find the actual speed of the rain in
.
Figure above depicts a situation when it's raining (as shown by arrows) and the man is moving on the track. Find the actual speed of the rain in
.
The answer is 5.77.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
While going down, rain is in the direction of his motion which is at 30 degrees to horizontal.
While moving up, he is at 60 degrees, rain at 30 degrees, and apparent, relative to him rain at 90 degrees.
So in a 30-60-90 right angled triangle, he is at 10 m/s leg, at 30 degrees with vertical hypotenuse.
So the other shorter leg at 60 to hypotenuse is 3 1 0 = \hgue 5 . 7 7 3 5 0 .
Checking on st. track confirms this.