This one could drive you buggy .....
Suppose 8 bugs are positioned at the 8 corners of a unit cube, (one bug per corner). Each bug, simultaneously, randomly and independently, chooses one of the 3 edges adjacent to its corner to travel on, and then does so until it reaches the next corner. (All the bugs travel at the same constant rate.)
The probability that none of the bugs meets any other bug in this process is b a , where a and b are positive coprime integers. Find a + b .
The answer is 2195.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I got 12/6561... :-(
Log in to reply
Close. :) I guess you missed one of the cases I outlined in my solution. It took me a long time to visualize the solution to this problem, but I think I have the right answer. I'm trying to visualize bugs moving on other Platonic solids now, so I may post similar questions in the future.
What about the case where the bugs traverse 3 points on one side (say the top, going clockwise from Top Front L corner to Top Back L corner to Top Back R corner), then leave that side and drop down to the bottom (Bottom Back R corner), go the other way (counter clockwise) to the Bottom Back L corner, Bottom Front L Corner, Bottom Front R corner, then go up to the Top Front R corner? Covers all corners, seems to add another 12 paths. Then there would be 36/6561 = 12/2187.
Log in to reply
Oh, never mind, I see: the bottom half makes a "U", so it reduces to one of the previous ones run backward.
lol i used a tissue box to help visualize
The best way to solve a combinatorics puzzle is to simulate it.
Label the vertices a, b, c, d, e, f, g and the edges 1 to 8 and create a directed graph like this.
 Imgur
Imgur
When a bug traverses an edge in the opposite direction, it's sign is taken to be negative. For example a path from D to C is -6
Now, let's make a list of all the 8-tuples which represent all possible ways the ants could go
1 2 3 4 5 6 7 8 9 10 |
|
Now, every valid path must not have two ants travelling in the same edge, i.e, must not contain a edge and it's negative. Also, it must not contain two edges that lead to the same vertex
1 2 3 4 5 6 7 8 9 10 11 12 |
|
We are ready!
1 2 |
|
So, there are 24 valid possibilities out of all 3 8 possibilities.
Thus required probability is 3 8 2 4
Sorry in lieu of a figure this is going to be long winded, but here we go -
The condition of Bugs not meeting can be viewed as 'find one or more uni-cursory paths to cover all vertices' Next consider the 'number of faces' taking part in these paths.
1.ONE FACE: If we take one face, 4 bugs take part and just move in a CW or CCW 'circle'. Then we need remaining 4 bugs to do the same on the opposite face. Giving 4 combinations (CW-CW, CW-CCW etc.) for one opposing face pair. Since there are 3 such pairs so in all 4 x 3 = 12 ways. 2. TWO FACES: If we take a loops with 2 faces, they will have to be adjacent, roping in 6 bugs. But then the remaining 2 will have to swap places along the edge they share, thereby meeting. So no solution here. 3. THREE FACES: 3.a. Three faces forming a 'C' clamp, gives us a uni-cursory path around the cube. Imagine instead of starting simultaneously, the bugs play 'tag' the next one to get him started. There are 6 ways we can 'C-clamp' the cube and then two direction to travel its edges. So another 6 x 2 = 12 ways! 3.b. Three faces forming a 'corner' isolate and leave one vertex high and dry. So no possibility of a solution here.
If I may give another way to program it in python, avoiding nested loops and so easily scalable:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
|
Log in to reply
You are indeed right. Nesting too many loops is not a good idea.
Thanks for your solution.
Let 1,2,3,4,1',2',3',4' be the bugs. There are 12 different 8-length cycles describing bug movements (such as 1-2-3-4-4'-3'-2'-1' - read: bug 1 goes towards bug 2, bug 2 towards bug 3, etc, bug 1' goes towards bug 1) and 12 different pairs of cycles of length 4 (such as 1-2-3-4, 1'-2'-3'-4') which gives bugs 24 ways to cross edges without meeting. We can pick two opposite sides of the cube in 3 ways and rotate bugs on each side clockwise or counterclockwise, so there are
3
∗
2
∗
2
=
1
2
(non ordered) pairs of 4-length cycles. It's not difficult to write down 12 8-length cycles if we draw our cube like a planar graph:
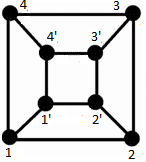 Since each bug can choose between 3 adjacent vertices, there are
3
8
permutations. Therefore, probability is
2
4
/
3
8
=
8
/
3
7
and the answer is
8
+
3
7
=
2
1
9
5
.
Since each bug can choose between 3 adjacent vertices, there are
3
8
permutations. Therefore, probability is
2
4
/
3
8
=
8
/
3
7
and the answer is
8
+
3
7
=
2
1
9
5
.
First, since each of the bugs has 3 edges it can travel along there are 3 8 = 6 5 6 1 possible patterns of motion for the 8 bugs.
For the bugs not to meet, there are two possibilities: (i) the pattern of all their moves combined forms two closed loops on opposite sides of the cube, and (ii) the pattern of all their moves combined forms a loop around the cube that visits each corner exactly once.
In case (i), there are 3 pairs of opposite sides, and each loop can go in one of two directions. This gives us 3 ∗ 2 ∗ 2 = 1 2 distinct patterns of motion.
In case (ii), we first note that at each corner exactly two adjacent edges must be on the loop, one leading to the corner and one leading away. If two such edges share a side of the cube, a third edge of that side must also be part of the loop in order for the loop to go through the last corner of that side before exiting that side. This forms a U -shape within the loop. (Note that the case where a 4 -th edge of a side is also part of the pattern of motion results in case (i), which we've already dealt with.)
Now to count these loops, we start by focussing on one corner. Two of the three adjacent edges must be part of the loop, which can be chosen in ( 2 3 ) = 3 ways. These two edges share a side, so as per the above discussion one of the remaining two edges must also be on the loop; once this choice is made, the rest of the loop can only be completed in one way. So there are 3 ∗ 2 = 6 possible loop paths, each of which can be traversed in one of two directions, resulting in a total of 6 ∗ 2 = 1 2 distinct patterns of motion.
Thus we end up with a desired probability of 6 5 6 1 1 2 + 1 2 = 2 1 8 7 8 . This means that a = 8 , b = 2 1 8 7 and a + b = 2 1 9 5 .