This only requires single variable calculus
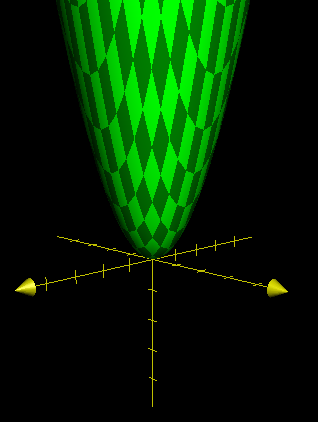
A circular paraboloid with equation z = x 2 + y 2 is being filled with water. When 10 cubic units of water have been added to the paraboloid, what will be the depth of the water? If D is the depth in units, find ⌊ 1 0 3 D ⌋ .
The answer is 2523.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Interesting! Thanks for sharing!
You can quickly realize that this paraboloid is merely finding the volume of revolution of a parabola. We could put this as y = x 2 revolved around the y-axis.
The formula for such a problem is ∫ 0 D π r 2 d y . D denotes the depth we are looking for. What is the radius r ? Remember, finding volumes of revolution is like finding the sum of volumes of infinite cylinders. Well, we are given y = x 2 and we need x in terms of y , so we could say x = y (it doesn't matter if you use the negative or positive version. I'm going to use positive version). Here, the x value always happens to be our radius. Also, why d y ? That would be the height of each cylinder, and this height lies on the y-axis.
The formula becomes:
∫ 0 D π y d y
= π 2 y 2 ∣ ∣ ∣ ∣ 0 D = π 2 D 2
Since the volume is 10, to solve for depth, set 10 equal to the equation we got.
1 0 = π 2 D 2 → D = π 2 0
⌊ 1 0 3 π 2 0 ⌋ = 2 5 2 3
It was known to Archimedes that the volume of a paraboloid is half the volume of the circumscribed cylinder. Thus π ( x 2 + y 2 ) z = π z 2 = 2 0 and z = π 2 0 ≈ 2 . 5 2 3 1 . The answer is 2 5 2 3 .