This OR That
The bitwise OR of two integers is the integer obtained by doing OR on each bit and concatenating them. Here is an example:
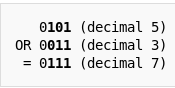
Chris has a list of 1 0 5 positive integers all of which are atmost 30 bits long. He wants to find out the sum of the bitwise OR for all possible pairs of them. However, due to the size of the input, he believes that it will take an awful lot of time.
Can you surprise him by finding the answer in reasonable time?
The answer is 3828434936185820379.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Here is my solution in Java. It is similar to Agnishom's solution. If n is the total number of integers, and a i is the number of these integers for which bit # i is set, then we have
-
2 1 a i ⋅ ( a i − 1 ) pairs in which both integers have this bit = 1;
-
n − a i pairs in which only one integer has this bit = 1.
Adding these together gives the number of terms (in my code called
pairs
) where this bit contributes to the sum.
Note:
ipf
is a BufferedReader opened to read the input file.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
|
A more intuitive and less mathematical way to code this is by keeping track of the number of pairs as we run through the list of integers. I declared another array
long p[] = new long[nB];
and write in the main loop:
1 2 3 4 |
|
The final summation is now easy, since
p[i]
is precisely the number of pairs whose ORed value has bit
#
i
equal to 1.
1 2 3 |
|
In the bitwise OR each bit is independent.
So we count how many numbers have the bit set in position 1, 2, ... and so on.
The same logic of Arjen Vreugdenhil solution,but in python.
1 2 3 4 5 6 7 8 9 10 11 12 |
|
Python code does make it short and crisp. Ain't it? Why the
# Happy Birthday
though?
Log in to reply
Today is my birthday.
Log in to reply
Oh, hey! Happy Birthday! May the force be with you!
Consider for a moment that all the inputs were just of 1 bit. Then, the OR of any two values is 0 iff both of them are 0. Otherwise, the OR is 1. So, the sum of the ORs is basically 2 n ( n − 1 ) − 2 c ( c − 1 ) where c is the number of 0s in the input.
Using this idea, we can solve the original problem bitwise. Consider the i t h bit of all the inputs. Every pair whose bitwise OR produces a 1 adds 2 i to the total sum. So, in essence, our answer is i ∑ 2 i ( 2 n ( n − 1 ) − 2 c [ i ] ( c [ i ] − 1 ) )
Inspiration