This purpose of this is show one how to do this type of problem #2

Calculus Level 3

This problem's question is What is the minimum distance between these two curves?

This time, the answer will not be given to you beforehand.

We will be working in Cartesian coordinates.

Curve 1: { x , 3 4 − x 2 2 } \left\{x,\frac{3 \sqrt{4-x^2}}{2}\right\} . This is an ellipse half.

Curve 2: { − 3 4 3 4 − x 2 − x 2 + 5 , − 3 4 − x 2 4 + 3 x 2 + 3 } \left\{-\frac{3}{4} \sqrt{3} \sqrt{4-x^2}-\frac{x}{2}+5,-\frac{3 \sqrt{4-x^2}}{4}+\frac{\sqrt{3} x}{2}+3\right\} , also an ellipse half, moved and rotated.

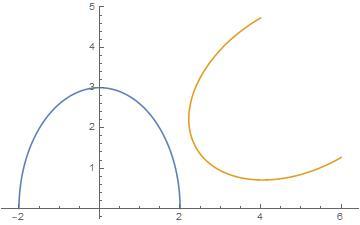
Just looking at the situation , one can see the answer is under 1.

Use calculus and the first and second derivatives of the Euclidean distance. I worked it out that way in the solution. We will be going directly for a numeric solution.


The answer is 0.608971133764103.

A Former Brilliant Member by A Former Brilliant Member

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

The red line segment shows the path of the shortest distance.

We want to avoid complex numbers. Therefore, we will constraint x and y to being between -2 and 2 inclusive. By restricting x and y in that way, absolute value functions do not need to surround the quantities being squared.

Here is a plot of the distance for varous values of x and y as restricted. Therefore, the distances are all real. The colors encode the relative distances from red being the furthest and violet being the closest. The white spot surrounds the minimum distance location on the distance surface.

dx = ∂ expr ∂ x ⇒ 3 x ( − 6 4 − x 2 − 3 4 − y 2 + 2 3 y + 12 ) 4 4 − x 2 + 2 ( x + 3 4 3 4 − y 2 + y 2 − 5 ) 2 1 16 ( − 6 4 − x 2 − 3 4 − y 2 + 2 3 y + 12 ) 2 + ( x + 3 4 3 4 − y 2 + y 2 − 5 ) 2 \text{dx}=\frac{\partial \text{expr}}{\partial x} \Rightarrow \\ \frac{\frac{3 x \left(-6 \sqrt{4-x^2}-3 \sqrt{4-y^2}+2 \sqrt{3} y+12\right)}{4 \sqrt{4-x^2}}+2 \left(x+\frac{3}{4} \sqrt{3} \sqrt{4-y^2}+\frac{y}{2}-5\right)}{2 \sqrt{\frac{1}{16} \left(-6 \sqrt{4-x^2}-3 \sqrt{4-y^2}+2 \sqrt{3} y+12\right)^2+\left(x+\frac{3}{4} \sqrt{3} \sqrt{4-y^2}+\frac{y}{2}-5\right)^2}}

dy = ∂ expr ∂ y ⇒ 1 8 ( 3 y 4 − y 2 + 2 3 ) ( − 6 4 − x 2 − 3 4 − y 2 + 2 3 y + 12 ) + 2 ( 1 2 − 3 3 y 4 4 − y 2 ) ( x + 3 4 3 4 − y 2 + y 2 − 5 ) 2 1 16 ( − 6 4 − x 2 − 3 4 − y 2 + 2 3 y + 12 ) 2 + ( x + 3 4 3 4 − y 2 + y 2 − 5 ) 2 \text{dy}=\frac{\partial \text{expr}}{\partial y} \Rightarrow \\ \frac{\frac{1}{8} \left(\frac{3 y}{\sqrt{4-y^2}}+2 \sqrt{3}\right) \left(-6 \sqrt{4-x^2}-3 \sqrt{4-y^2}+2 \sqrt{3} y+12\right)+2 \left(\frac{1}{2}-\frac{3 \sqrt{3} y}{4 \sqrt{4-y^2}}\right) \left(x+\frac{3}{4} \sqrt{3} \sqrt{4-y^2}+\frac{y}{2}-5\right)}{2 \sqrt{\frac{1}{16} \left(-6 \sqrt{4-x^2}-3 \sqrt{4-y^2}+2 \sqrt{3} y+12\right)^2+\left(x+\frac{3}{4} \sqrt{3} \sqrt{4-y^2}+\frac{y}{2}-5\right)^2}}

The method of gradient descent can be used to find the minimum. If the derivatives are too complex to compute symbolically, then they also can be approximated by the f ( x ) − f ( x + δ x ) δ x \frac{f(x)-f(x+\delta x)}{\delta x} method.

Solving dx = 0 ∧ dy = 0 \text{dx}=0\land \text{dy}=0 result in only one real solution: x → 1.73938727080588 , y → 0.0.216468353808727 x\to 1.73938727080588,y\to 0.0.216468353808727 .

Substituting those values back into the original distance formula gives the minimum distance of 0.608971133764102.

Sometimes, it is easier to sketch graph the situation and estimate the minimum distance and the pick out the minimum from the saddle point and the maximum. In these problem, I avoided that need.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...