This question got some attention these past few days

There are 60 seconds in a minute, 60 minutes in an hour, 24 hours in a day, 7 days in a week. Hence $n!=60\times 60\times 24\times 7\times 6$ . We know that $n!$ contains $2$ factors of $5$ , hence $n\geq 10$ . However, $n!$ does not contain a factor of $11$ , hence $n<11$ . Conclusion: $n=\boxed{10}$ .

Since 1 week has 7 days , each day has 24 hours , each hour has 60 minutes and each minute has 60 seconds , Total seconds in 6 weeks are:

$6 \times 7 \times 24 \times 60 \times 60 \\ = 6 \times 7 \times 4 \times 3 \times 2 \times 1 \times (5 \times 4 \times 3) \times (5 \times 2 \times 2 \times 3) \\ = 1 \times 2 \times 3 \times 4 \times 5 \times 6 \times 7 \times (4\times 2) \times (3 \times 3) \times (5 \times 2)\\ = 10!$

For those who know right off the bat that $24$ is equal to $4!$ , it becomes apparent that we are almost finished calculating up to an $n$ of $7$ already since there are $24$ hours in a day, $7$ days in a week, and $6$ weeks to solve for:

$7! = 4! \times 7 \times 6 \times 5$ .

We have everything except a $5$ to complete our calculation up to $7!$ The only thing left to do, then, is to isolate a factor of 5 from what's left to solve. What's left is the number of seconds in an hour, which we can quickly determine to be $3600$ .

Thus, $n! = 7 \times 6 \times 5 \times 4! \times \frac{3600}{5} \rightarrow 7! \times 720 \rightarrow 7! \times (8 \times 9 \times 10) \rightarrow 10!$

$\boxed{n = 10}$

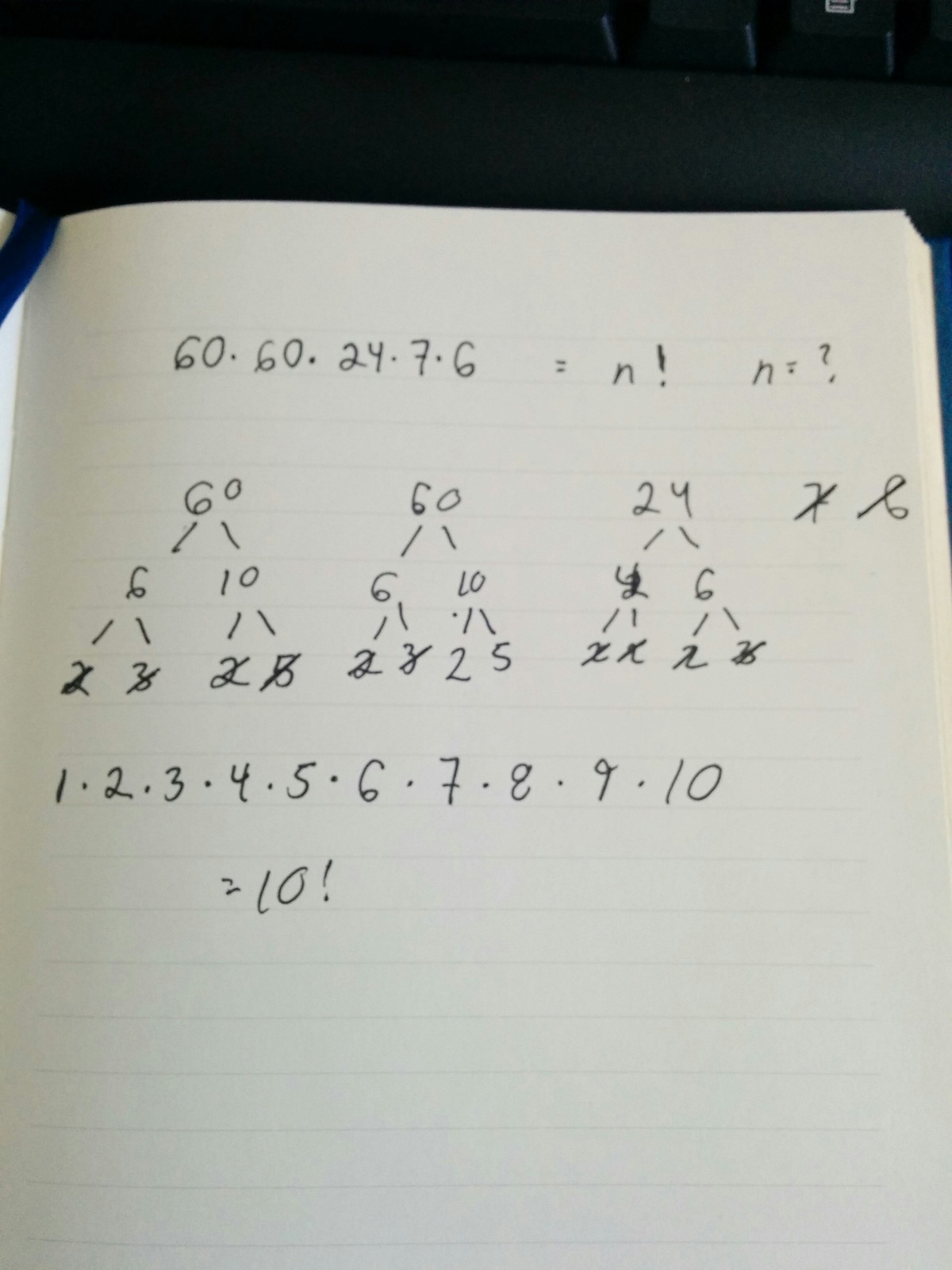
I used prime factorization to break down 60 and 24, and then, starting with 1, worked my way through the whole numbers, crossing out primes as I used them.

Not entirely sure this method is pretty valid, but just know that

6 weeks = 6 * 7 days = 6 * 7 * 24 hours = 6 * 7 * 24 * 60 minutes = 6 * 7 * 24 * 60 * 60 seconds. = n! seconds.

Now just continue dividing that number with increasing integers starting from 1.

$(6)(7)(24)(60)(60) \over {1}$ $= (6)(7)(24)(60)(60)$

$(6)(7)(24)(60)(60) \over {2}$ $= (3)(7)(24)(60)(60)$

$(3)(7)(24)(60)(60) \over {3}$ $= (1)(7)(24)(60)(60)$

$(1)(7)(24)(60)(60) \over {4}$ $= (1)(7)(6)(60)(60)$

$(1)(7)(6)(60)(60) \over {5}$ $= (1)(7)(6)(12)(60)$

$(1)(7)(6)(12)(60) \over {6}$ $= (1)(7)(1)(12)(60)$

$(1)(7)(1)(60)(60) \over {7}$ $= (1)(1)(1)(12)(60)$

$(1)(1)(1)(720) \over {8}$ $= (1)(1)(1)(90)$

$(1)(1)(1)(90) \over {9}$ $= (1)(1)(1)(10)$

$(1)(1)(1)(10) \over {10}$ $= (1)(1)(1)(1))=1$

Since $(n!) \over {(1)(2)(3)(4)(5)(6)(7)(8)(9)(10)}$ = $(n!) \over {10!}$ $= 1$ , $n! = 10!$ .

Hence $\boxed {n=10}$ .

Seconds of 6 week = 6 7 24 60 60=6 7 (8 3) (3 4 5) (2 3 10)=10 9 8 7 6 5 4 3 2 1=10! So n=10

6 weeks in days is $6 \times 7 = 42$ .

Then $60 \times 60 \times 24 \times 42$ .

Factoring, then $2 \times 2 \times 3 \times 5 \times 2 \times 2 \times 3 \times 5 \times 2 \times 2 \times 2 \times 3 \times 2 \times 3 \times 7$ .

So, $2 ^ { 8 } \times 3 ^ { 4 } \times 5 ^ { 2 } \times 7$ .

$( 2 \times 5 ) \times ( 3 ^ { 2 } ) \times ( 2 ^ { 3 } ) \times 7 \times ( 2 \times 3 ) \times 5 \times ( 2 ^ { 2 } ) \times 3 \times 2 \times 1 = 10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1 = 10!$ .

So, $n! = 10!$ .

Hence, the answer is $\boxed { 10 }$ .

First attack the problem backward.

$7$ weeks $=$ $7 \times 6$ days

$7 \times 6$ days $=$ $7 × 6 × 24$ hours $=$
$7 \times 6 \times 4!$ hours

$7 \times 6 \times 4!$ hours $=$ $7 \times 6 \times 4! × 60$ minutes $=$ $7 \times 6 \times 5 \times 4! \times 12$ minutes $=$ $7! \times 12$ minutes

$7! \times 12$ minutes $=$ $7! \times 12 \times 60$ seconds $=$ $10 \times 9 \times 8 \times 7!$ second $=$ $10!$ seconds

So $n!$ $= 10!$ $,n = \boxed{10}$

The number of seconds in 6 weeks is , $n!=\color{#D61F06}{6}\times\color{#20A900}{7}\times\color{#3D99F6}{24}\times\color{#CEBB00}{60}\times\color{#69047E}{60}\\=\color{#D61F06}{6}\times\color{#20A900}{7}\times\color{#3D99F6}{4\times3\times2}\times\color{#CEBB00}{5\times3\times4}\times\color{#69047E}{2\times10\times3}\\ =\color{#3D99F6}{2\times3\times4}\times\color{#CEBB00}{5}\times\color{#D61F06}{6}\times\color{#20A900}{7}\times\color{#333333}{(}\color{#CEBB00}{4}\times\color{#69047E}{2}\color{#333333}{)}\times\color{#333333}{(}\color{#CEBB00}{3}\times\color{#69047E}{3}\color{#333333}{)}\times\color{#69047E}{10}\\=2\times3\times4\times5\times6\times7\times8\times9\times10=10!$

$n!=10!\\\boxed{n=10}$

We have 3600×24×7×6 There are two factors 5 but there isn't the 11, thus the value of n must be 10.

total number of seconds, n!=6 7 24*3600 hence 9<n<15,
also 11 is not a factor n!, hence n!=10

1 week has 7 days , each day has 24 hours , each hour has 60 minutes and each minute has 60 seconds , Total seconds in 6 weeks are: 6x7x24x60x60= 3628800 1x(2x3)x7x(6x4)x5x8x9x10 = 10!

Answer is n = 10 The duration is 60 sec/min x 60 min/hr x 24 hr/day x 7 day/week x 6 weeks = (2x2x3x5) x (2x2x3x5) x (2x2x2x3) x (7) x (2x3) sec. I need a 7 (largest prime) so n! >= 7! = (1) x (2) x (3) x (2x2) x (5)x (2x3) x (7) After simplifying I get: (5) x (2x2x2x3) x (2x3) sec. I need another 5 so n! >= 10! 10! -7! = (2x2x2) x (3x3) x (2x5) After simplifiyng nothing is left so n = 10 Look Mah, no calculator!