This should be easy! Right? Part - 3

Geometry Level 5

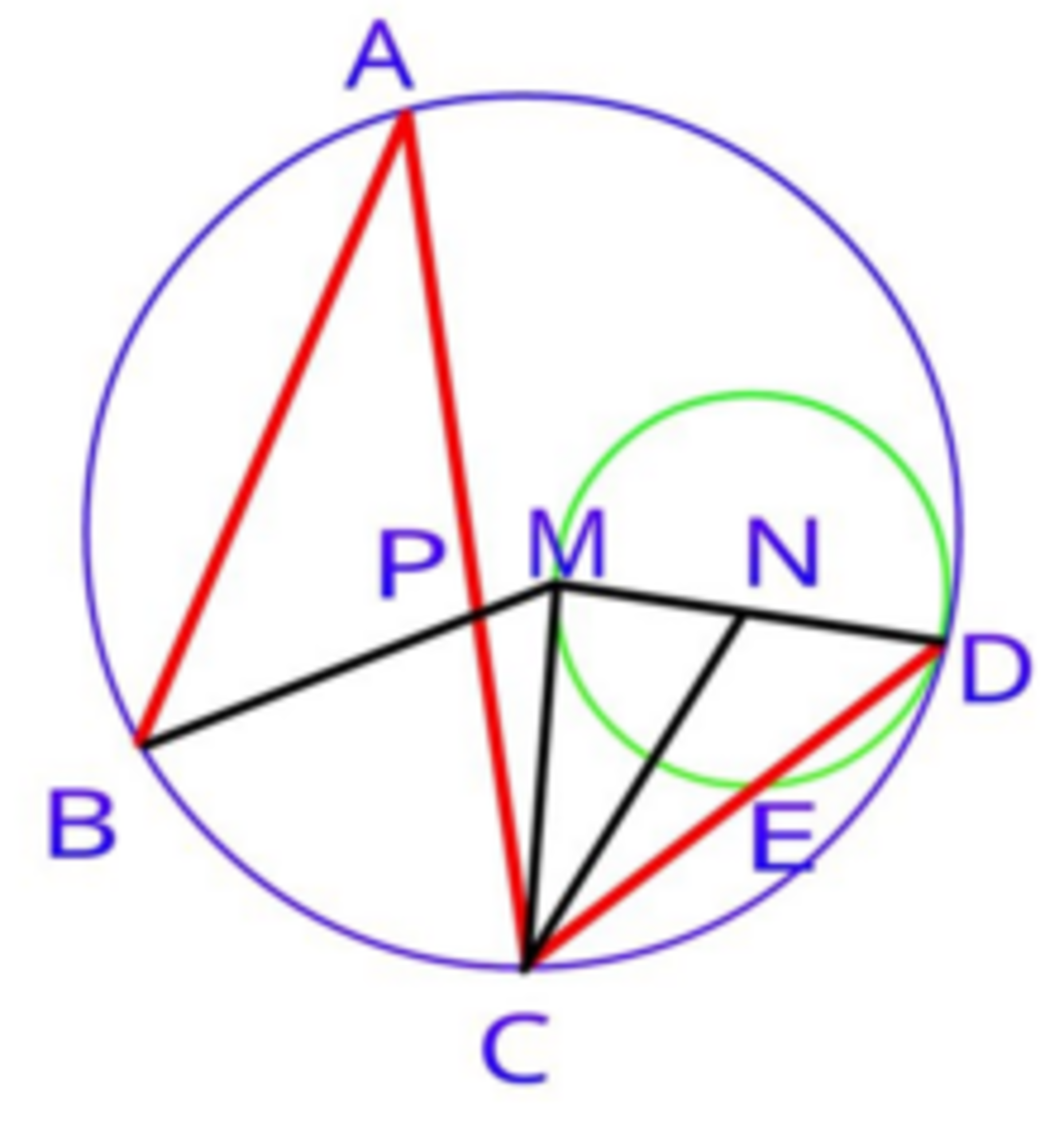
The figure above represents two circles where A B = 5 AB=5 units, ∠ B A C = 3 0 ∘ \angle BAC=30^\circ , ∠ B M D = 13 5 ∘ \angle BMD=135^\circ , M D = 3.3 MD = 3.3 units and N N is the mid point of M D MD .

C D C N × C M = a c − d + e b e b − d + e \dfrac{CD}{CN}\times{CM}=\frac{a\sqrt{c-\sqrt{d}+\sqrt{e}}}{b\sqrt{e}\sqrt{b-\sqrt{d}+\sqrt{e}}}

The equation above holds true for positive integers a , b , c , d a,b,c,d and e e with b , d b,d and e e square-free, a > b a>b , and a , b a,b are coprime.

Find a + b + c + d + e a+b+c+d+e .

Clarification : M D MD a diameter of the smaller circle. M M is the centre of the larger circle. The two circles tangential at D D .

Try Part-1 and Part-2 also.


The answer is 50.

Akshay Yadav by Akshay Yadav , 20, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

First let the radius of the bigger circle to be r and let the angle between sides MD and MC be θ \theta .

Then,

C D 2 = 2 r 2 − 2 r 2 cos ⁡ θ \displaystyle { CD }^{ 2 }=2{ r }^{ 2 }-2{ r }^{ 2 }\cos { \theta }

C N 2 = r 2 + r 2 4 − r 2 cos ⁡ θ \displaystyle { CN }^{ 2 }={ r }^{ 2 }+\frac { { r }^{ 2 } }{ 4 } -{ r }^{ 2 }\cos { \theta }

C M 2 = r 2 \displaystyle { CM }^{ 2 }={ r }^{ 2 }

C D 2 C N 2 × C M 2 = 2 r 2 ( 1 − cos ⁡ θ ) r 2 ( 5 4 − cos ⁡ θ ) × r 2 \displaystyle \frac { { CD }^{ 2 } }{ { CN }^{ 2 } } \times { CM }^{ 2 }=\frac { 2{ r }^{ 2 }\left( 1-\cos { \theta } \right) }{ { r }^{ 2 }\left( \frac { 5 }{ 4 } -\cos { \theta } \right) } \times { r }^{ 2 }

θ = 135 − 2 × 30 = 75 = 30 + 45 \displaystyle \theta = 135-2 \times 30=75=30+45 . Because BMC is twice BAC by the Euclidean geometry theorem.

cos ⁡ θ = cos ⁡ 45 + 30 = 3 − 1 2 2 \displaystyle \cos { \theta } =\cos { 45+30 } =\frac { \sqrt { 3 } -1 }{ 2\sqrt { 2 } }

C D 2 C N 2 × C M 2 = 2 r 2 ( 1 − cos ⁡ θ ) r 2 ( 5 4 − cos ⁡ θ ) × r 2 = 2 ( 1 − ( 3 − 1 ) 2 2 ) ( 5 4 − ( 3 − 1 ) 2 2 ) × r 2 \displaystyle \frac { { CD }^{ 2 } }{ { CN }^{ 2 } } \times { CM }^{ 2 }=\frac { 2{ r }^{ 2 }\left( 1-\cos { \theta } \right) }{ { r }^{ 2 }\left( \frac { 5 }{ 4 } -\cos { \theta } \right) } \times { r }^{ 2 }=\frac { 2\left( 1-\frac { \left( \sqrt { 3 } -1 \right) }{ 2\sqrt { 2 } } \right) }{ \left( \frac { 5 }{ 4 } -\frac { \left( \sqrt { 3 } -1 \right) }{ 2\sqrt { 2 } } \right) } \times { r }^{ 2 }

= 2 ( 4 − 6 − 2 ) ( 5 − 6 − 2 ) × r 2 \displaystyle =\frac { 2\left( 4- \sqrt { 6 } - \sqrt { 2 } \right) }{ \left( 5 -\sqrt { 6 } - \sqrt { 2 } \right) } \times { r }^{ 2 }

r = 3.3 = 33 10 \displaystyle r=3.3=\frac{33}{10}

= 2 ( 4 − 6 − 2 ) ( 5 − 6 − 2 ) × ( 33 10 ) 2 \displaystyle =\frac { 2\left( 4- \sqrt { 6 } - \sqrt { 2 } \right) }{ \left( 5 -\sqrt { 6 } - \sqrt { 2 } \right) } \times { \left( \frac { 33 }{ 10 } \right) }^{ 2 }

C D C N × C M = = 2 ( 4 − 6 − 2 ) ( 5 − 6 − 2 ) × ( 33 10 ) 2 \displaystyle \frac { { CD } }{ { CN } } \times { CM }==\sqrt { \frac { 2\left( 4- \sqrt { 6 } - \sqrt { 2 } \right) }{ \left( 5 -\sqrt { 6 } - \sqrt { 2 } \right) } \times { \left( \frac { 33 }{ 10 } \right) }^{ 2 } }

= 2 ( 4 − 6 − 2 ) ( 5 − 6 − 2 ) × ( 33 10 ) \displaystyle =\sqrt { \frac { 2\left( 4- \sqrt { 6 } - \sqrt { 2 } \right) }{ \left( 5 -\sqrt { 6 } - \sqrt { 2 } \right) } } \times { \left( \frac { 33 }{ 10 } \right) }

= ( 4 − 6 − 2 ) ( 5 − 6 − 2 ) × ( 33 5 2 ) \displaystyle =\sqrt { \frac { \left( 4- \sqrt { 6 } - \sqrt { 2 } \right) }{ \left( 5 -\sqrt { 6 } - \sqrt { 2 } \right) } } \times { \left( \frac { 33 }{ 5\sqrt { 2 } } \right) }

= ( 33 5 2 ) × ( 4 − 6 − 2 ) ( 5 − 6 − 2 ) \displaystyle = { \left( \frac { 33 }{ 5\sqrt { 2 } } \right) }\times \sqrt { \frac { \left( 4- \sqrt { 6 } - \sqrt { 2 } \right) }{ \left( 5 -\sqrt { 6 } - \sqrt { 2 } \right) } }

= ( 33 5 2 ) × ( 4 − 6 − 2 ) ( 5 − 6 − 2 ) = ( a b e ) × ( c − d − e ) ( b − d − e ) \displaystyle = { \left( \frac { 33 }{ 5\sqrt { 2 } } \right) }\times \sqrt { \frac { \left( 4- \sqrt { 6 } - \sqrt { 2 } \right) }{ \left( 5 -\sqrt { 6 } - \sqrt { 2 } \right) } } = { \left( \frac { a }{ b\sqrt { e } } \right) }\times \sqrt { \frac { \left( c- \sqrt { d } - \sqrt { e } \right) }{ \left( b -\sqrt { d } - \sqrt { e } \right) } }

So,

a = 33 , b = 5 , c = 4 , d = 6 , e = 2 \displaystyle a=33,b=5,c=4,d=6,e=2

a + b + c + d + e = 33 + 5 + 4 + 6 + 2 = 50 \displaystyle a+b+c+d+e=33+5+4+6+2=\boxed{50}

3 Helpful 0 Interesting 0 Brilliant 0 Confused

Thanks for posting a solution to my problem. I thought no will be willing to do so and in the end I will have to do it myself.

Akshay Yadav - 5 years, 3 months ago

Log in to reply

Is there a better / more direct approach to this problem? I quite like it, but this solution makes it look really painful

Calvin Lin Staff - 5 years, 3 months ago

Log in to reply

Sir, when I was making this problem, even I used the same method as given in the solution of @คลุง แจ็ค

Akshay Yadav - 5 years, 3 months ago

Is this your own problem ? It is really cool.

Venkata Karthik Bandaru - 5 years, 3 months ago

Log in to reply

Yeah! Its 100% original problem. Thanks.

Akshay Yadav - 5 years, 3 months ago

Great problem. But isn't there any approach that uses less computations?

A Former Brilliant Member - 5 years, 2 months ago

Log in to reply

Even I did it the same way as given in the solution, you can say that I deliberately made it so that its calculations are hard to do.

Akshay Yadav - 5 years, 2 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...