This should've been mechanics!
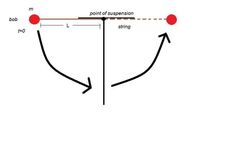 Consider a
mathematical pendulum
. It is held at a position as shown above at
t
=
0
, before it is released. Find the time taken by it to complete one oscillation, that is the time taken by it to make a complete round from its initial position to back to the initial position. If the time taken can be represented as:
Consider a
mathematical pendulum
. It is held at a position as shown above at
t
=
0
, before it is released. Find the time taken by it to complete one oscillation, that is the time taken by it to make a complete round from its initial position to back to the initial position. If the time taken can be represented as:
π β g γ L α Γ δ ( η 1 )
where Γ is the gamma function and α , β , γ , δ , and η are all positive integers . Find α + β + γ + η δ .
The answer is 19.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
This all comes down to conservation of energy. We have:
2 1 m v 2 = m g L cos θ ⇒ v ( θ ) = 2 g L cos θ ⇒ v ( θ ) 1 = 2 g L cos θ 1
In order to get the period, we have to evaluate the following integral:
T = ∫ s 1 s 2 v ( s ) 1 d s
We do a change of variables to θ . Since θ = L s ⇒ s = θ L , we get:
T = ∫ θ 1 θ 2 v ( θ ) 1 L d θ
Integrating from 2 π to 0 , we get one fourth of the period, thus:
T = 4 ∫ 0 2 π v ( θ ) L d θ = 4 ∫ 0 2 π 2 g L cos θ L d θ = 2 g 2 L ∫ 0 2 π cos θ 1 = g 2 L B ( 2 1 , 4 1 )
⇒ g 2 L Γ ( 4 3 ) Γ ( 2 1 ) Γ ( 4 1 ) = π g L Γ ( 4 1 ) 2
So we have:
α + β + γ + η δ = 1 + 1 + 1 + 4 2 = 1 9
If θ is the angle that the string of the pendulum makes with the downward vertical, then conservation of energy tells us that 2 1 m L 2 θ ˙ 2 + m g L ( 1 − cos θ ) = m g L and hence that θ ˙ 2 = L 2 g cos θ Solving this differential equation, the period of the oscillation is T = 2 ∫ − 2 1 π 2 1 π 2 g L cos θ d θ = g 8 L ∫ 0 2 1 π cos θ d θ = g 8 L ∫ 0 2 1 π cos θ ( 1 − cos 2 θ ) sin θ d θ With the substitution u = cos 2 θ this becomes T = g 2 L ∫ 0 1 u − 4 3 ( 1 − u ) − 2 1 d u = g 2 L B ( 4 1 , 2 1 ) Since Γ ( 2 1 ) = π and Γ ( 4 1 ) Γ ( 4 3 ) = sin 4 1 π π = π 2 , it follows that T = π g L Γ ( 4 1 ) 2 making the answer 1 + 1 + 1 + 4 2 = 1 9 .