This world needs more coin of such shape!
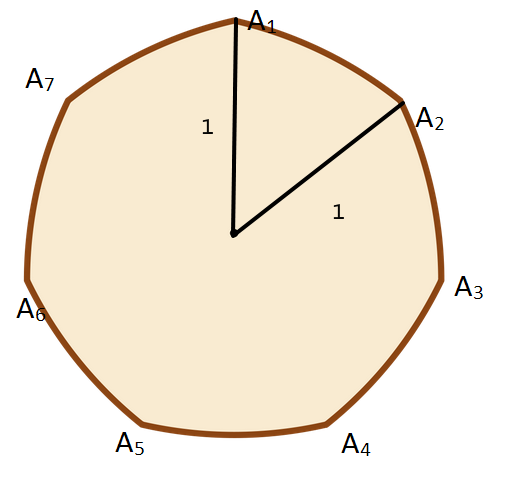 The diagram above shows a Reuleaux septagon drawn from a regular septagon with circumradius 1, where arc
A
1
A
2
is drawn from center
A
5
, arc
A
2
A
3
is drawn from center
A
6
, arc
A
3
A
4
is drawn from center
A
7
, and so on.
The diagram above shows a Reuleaux septagon drawn from a regular septagon with circumradius 1, where arc
A
1
A
2
is drawn from center
A
5
, arc
A
2
A
3
is drawn from center
A
6
, arc
A
3
A
4
is drawn from center
A
7
, and so on.
Find the area of the Reuleaux septagon to 5 decimal places.
Bonus : Generalize this for all Reuleaux n -gon where n is an odd number.
You may want to read up Reuleaux triangle first.
Image Credit: Wikimedia Reuleaux polygons by LEMeZza
The answer is 2.93488.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
<A1:O:A2 has two values.
Area of Reuleaux n -gon, when n is an odd positive integer, when R is the circumradius of associated regular n -gon,
2 1 n R 2 ( sin n 2 π + 4 ( 2 n π − sin 2 n π ) × cos 2 2 n π )
Further algebraic simplification may be possible.
Wow, I lost my original working for the "Bonus" question, but I think this expression looks correct.
Log in to reply
Thank you!
Ya it is correct and the most appropriate method.
∠ A 1 O A 2 = 7 2 π
∠ A 1 A 5 A 2 = 7 π
∠ A 1 O A 2 = 1 4 π
∠ A 1 O A 5 = 7 6 π
Area triangle A 1 O A 5 = 2 1 sin 7 6 π
Length A 1 A 5 = sin 1 4 π sin 7 6 π
Area sector A 1 A 5 A 2 = 2 1 ∠ A 1 A 5 A 2 × ( A 1 A 5 ) 2
Area bounded by radii O A 1 , O A 2 and arclength A 1 A 2 = Area sector A 1 A 5 A 2 - 2 Area triangle A 1 O A 5
= 1 4 π sin 2 7 6 π ÷ sin 2 1 4 π - sin 7 6 π
Area Reuleaux heptagon is 7 × this =2.93488
Check: upper bound π , Lower bound 2 7 sin 7 2 π =2.73641
Similarly for odd Reuleaux n-gon
Area n-gon
= 2 n π sin 2 n ( n − 1 ) π ÷ sin 2 2 n π − sin n ( n − 1 ) π
Sorry about the clunkiness of the typesetting ; I'm a 46 year old LaTeX virgin (no sniggering at the back there). Next time I'll just upload a photo.