This year is always better than last year?(2)
Let the area between the circumcircle and the incircle of an unit n -gon (side length equals to 1) be f ( n ) .
What is the relationship between f ( 2 0 1 7 ) and f ( 2 0 1 8 ) ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
This is a version of the classic geometry puzzle where all you have is the chord of an annulus, and you need to find its area: https://brilliant.org/problems/fun-time-2/ .
The area of the circumcircle is π ⋅ B O 2 , and the area of the incircle is π ⋅ C O 2 , so the difference is π ⋅ B O 2 − π ⋅ C O 2 . By Pythagoras, B O 2 − C O 2 = B C 2 = 4 1 , so the area is simply 4 π .
Relevant wiki: Pythagorean Theorem
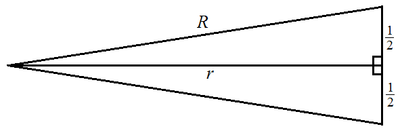 Consider an isosceles triangle formed by one side of the unit regular
n
-gon with the center of the
n
-gon. Let the circumradius and inradius of the
n
-gon be
R
and
r
respectively. By Pythagorean theorem, we have
R
2
=
r
2
+
(
2
1
)
2
=
r
2
+
4
1
. Now, we have
f
(
n
)
=
π
R
2
−
π
r
2
=
π
(
r
2
+
4
1
−
r
2
)
=
4
π
. Implying that
f
(
n
)
=
4
π
for all
n
. Therefore,
f
(
2
0
1
7
)
=
f
(
2
0
1
8
)
.
Consider an isosceles triangle formed by one side of the unit regular
n
-gon with the center of the
n
-gon. Let the circumradius and inradius of the
n
-gon be
R
and
r
respectively. By Pythagorean theorem, we have
R
2
=
r
2
+
(
2
1
)
2
=
r
2
+
4
1
. Now, we have
f
(
n
)
=
π
R
2
−
π
r
2
=
π
(
r
2
+
4
1
−
r
2
)
=
4
π
. Implying that
f
(
n
)
=
4
π
for all
n
. Therefore,
f
(
2
0
1
7
)
=
f
(
2
0
1
8
)
.
Let B be a vertex and C be a midpoint of one of the sides of a unit n -gon, and let O be the center. Then B , O , and C make a right triangle △ B O C , where B C = 2 1 and ∠ B O C = n π , and B O is the radius of the circumcircle and C O is the radius of the incircle.
By trigonometry, B O = 2 1 csc n π and C O = 2 1 cot n π . Since B O is the radius of the circumcircle and C O is the radius of the incircle, the area between the circles is f ( n ) = π B O 2 − π C O 2 = 4 π csc 2 n π − 4 π cot 2 n π = 4 π ( csc 2 n π − cot 2 n π ) .
However, since csc 2 θ − cot 2 θ = 1 , this area can be simplified to f ( n ) = 4 π , which is a constant with respect to the number of sides n of the polygon. Therefore, f ( 2 0 1 7 ) = f ( 2 0 1 8 ) .