Those are some friendly numbers

Since in each friendly pair the two numbers have the same greater digit, we can easily construct a maximal set of pairwise unfriendly numbers for each greater digit.

The numbers with greater digit 9 are 19, 29, 39, 49, 59, 69, 79, 89, 99, 98, 97, 96, 95, 94, 93, 92, 91 In this list, each adjacent pair is friendly, therefore taking every other number gives an upper bound for the number of pairwise unfriendly numbers we can find in this list. Indeed, taking every other number satisfies this requirement: the 9-element set {19, 39, 59, 79, 99, 97, 95, 93, 91} obviously contains no friendly pair.

In the same way, the 8-element set {18, 38, 58, 78, 87, 85, 83, 81} is the maximal set for numbers with greater digit 8.

This pattern continues, down to the set {11} for greater digit 1, therefore the total is $\sum_{r=1}^9 r = \boxed{45}$ .

The largest possible subset has 45 elements, which can be attained using the following construction.

• Take the 17 numbers whose smallest digit is 1 - namely, $11, 12, 13, 14, 15, 16, 17, 18, 19, 21, 31, 41, 51, 61, 71, 81, 91$ .

• Take the 13 numbers whose smallest digit is 3 - namely, $33, 34, 35, 36, 37, 38, 39, 43, 53, 63, 73, 83, 93$ .

• Take the 9 numbers whose smallest digit is 5 - namely, $55, 56, 57, 58, 59, 65, 75, 85, 95$ .

• Take the 5 numbers whose smallest digit is 7 - namely, $77, 78, 79, 87, 97$ .

• Take the 1 numbers whose smallest digit is 9 - namely, $99$ .

Now, consider the diagram below, where each square represents one of the numbers in $S$ . We consider the square in row $i$ and column $j$ to denote the 2 digit number $\overline{ij}$ .

Nine of the squares are shaded grey, while the remaining 72 squares are divided into 36 pairs.

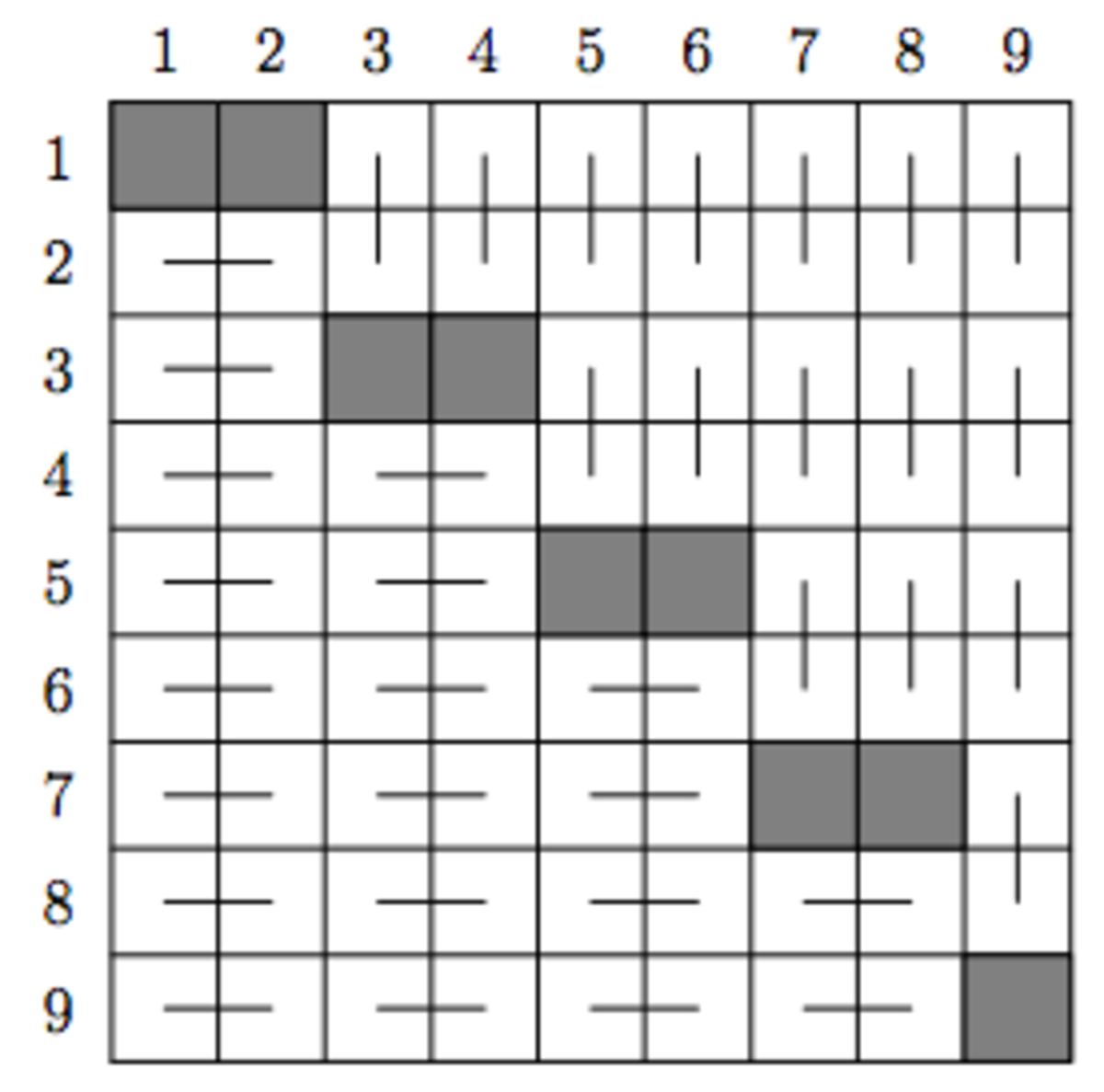
It is easy to check that each of these pairs denotes two friendly numbers. Therefore, at most one of the elements in each pair can be in our set. Also, the 9 shaded square are not friendly either.

Therefore, we have a maximum of $36+9=\boxed{45}$ elements in our set.