Those long summer days...
Estimate the time difference between the longest amount of daylight in one day and the shortest amount of daylight on one day in seconds over the course of a year if you lived on the Earth's equator with the assumptions below.
Note: this is not the difference between solstices as we are adjusting the earth's rotation axis to be perpendicular to the orbital plane.
Details and assumptions
-
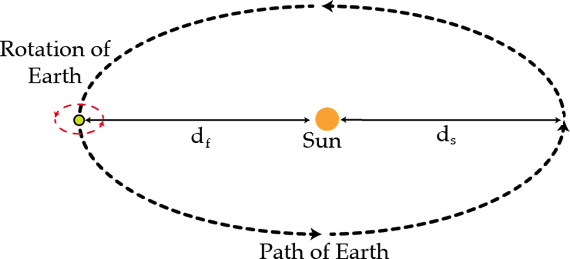
The furthest distance from the Sun to Earth is d f = 1 . 5 2 1 × 1 0 8 km .
-
The shortest distance from the Sun to Earth is d s = 1 . 4 7 × 1 0 8 km .
-
To simplify the problem, assume that the Earth's axis is always perpendicular to the plane of its trajectory around the Sun.
-
The Sun always shines on half of the Earth.
-
There are 24 hours in a day and 365.25 days in a year.
The answer is 16.13.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The Earth goes around the Sun in T = 3 6 5 . 2 5 days and rotates around its axis in t = 1 day. These two motions are in opposite directions. Since the angular momentum of the earth around the sun is a constant of motion and L ∼ r 2 ω , ω ∼ r − 2 and the different angular velocities when the earth is close or far from the Sun is Δ ω = T 2 π ( d f 2 − d s 2 ) / d 0 2 where d 0 is the average of d f and d s .
As the earth spins it also goes around the sun, which means that if the period of the earth's spin is t, the total angle seen during daylight is π + β , β = − ω t . The length of daylight t d is therefore
t d = 2 π π + β t .
The difference in t d during the longest and shortest day of the year is then
t l − t s = 2 π Δ ω t 2 ,
which works out to be 16.13 seconds.
the sun cause an angular shift in one day I 'll calculate it then I'll compare the maximum with the minimum value of it. the sun's Mass we can calculate it using Kepler's third Law a 3 T 2 = G M 4 π 2 then from the mechanical Energy equation for planets motion E = − 2 a G M m here E = 2 1 m v 2 − D G M m so v = G M a D 2 a − D we all know "according to kepler's laws" that the velocity at the nearest point is the biggest and at the furthest point is the smallest so V is the biggest and v is the smallest then
V = G M a D ′ 2 a − D ′ here D ′ = 1 . 4 7 ∗ 1 0 8 k m
and we have v = G M a d 2 a − d here d = 1 . 5 2 1 ∗ 1 0 8 k m the angular shift for each case is
δ θ ′ = D ′ T V
where T = 2 4 ∗ 3 6 0 0 s e c
δ θ = d T v so the shift in seconds in each case is Δ τ ′ = T 2 π δ θ ′
Δ τ = T 2 π δ θ
Δ τ ′ − Δ τ = 1 6 . 1 3 s e c