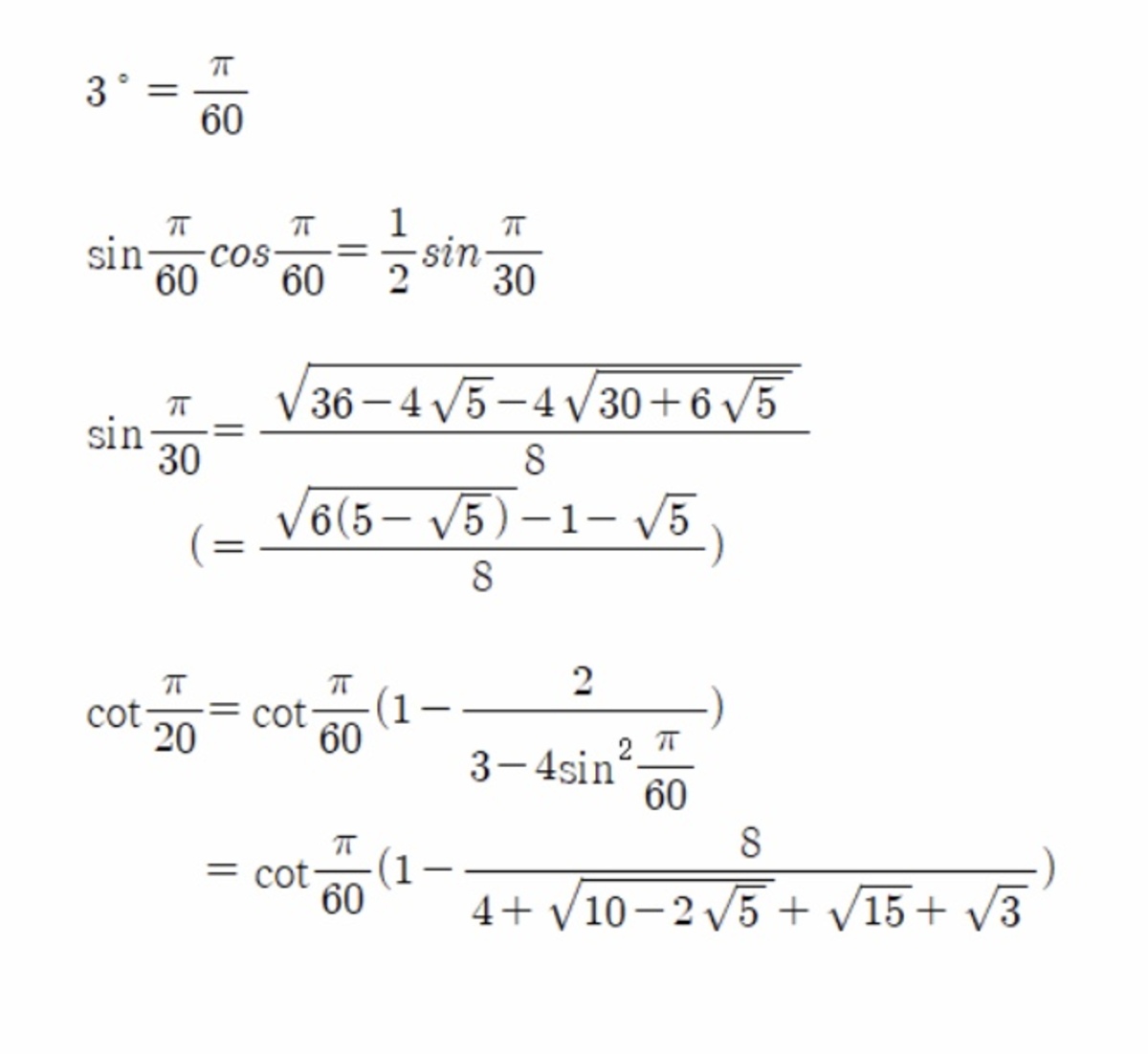Those nested radicals

Calculus Level 5

$\lim_{n\to \infty}\operatorname{cot}\left(\pi\sqrt{100n^2+n+1}\right)$

For integer $n$ , the limit above can be expressed as

$\frac{a\cos^2(3^{\circ})}{\sqrt{b-4\sqrt{5}-4\sqrt{30+6\sqrt{5}}}}\left(1-\frac{c}{4+\sqrt{10-2\sqrt 5}+\sqrt{15}+\sqrt{3}}\right)$

where $a$ , $b$ , and $c$ are positive integers with $a$ and $b$ being perfect squares. Find $a+b+c$ .

1 solution

Ramanujan Incarnation of the great
Oct 8, 2020

This problem can be solved easily as the following. For all integers $n$ , $\cot(n\pi+x)=\cot{x}$ . Since $\cot{x}$ is a continuous function,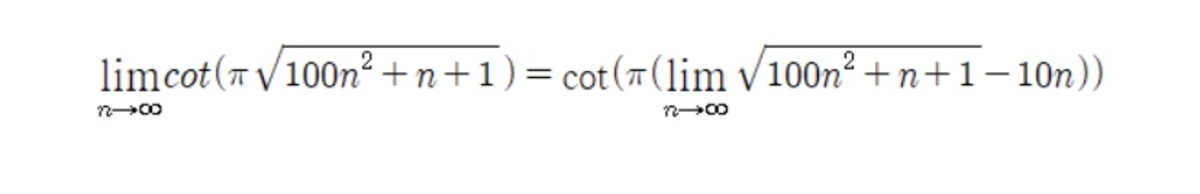

Thus the answer is $\cot (\dfrac{\pi}{20})$ .

Here are some guides for getting the final result $a=16, b=36, c=8$ (The following steps seem trivial.)